こちら↓で解説したように、最小二乗法による線形重回帰分析 (Ordinary Least Squares, OLS), リッジ回帰 (Ridge Regression, RR), Least Absolute Shrinkage and Selection Operator (LASSO), Elastic Net (EN) はとても似ています。
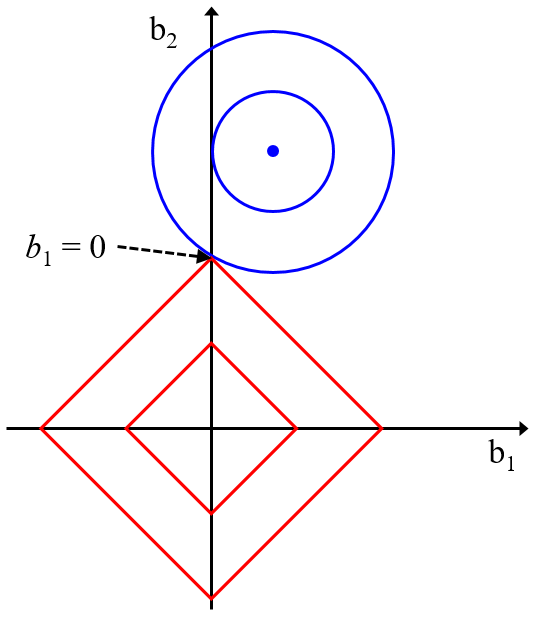
OLS では目的変数 y の誤差の二乗和のみ小さくするよう回帰係数が計算され、RR, LASSO, EN ではそれに加えて回帰係数の値も一緒に小さくするように回帰係数が計算されます。さらに言えば EN で最小化する項には、RR の項と LASSO の項がどちらも含まれており、その重み α を調整すれば、α = 1 のときに RR とまったく同じ式になり、α = 0 のときに LASSO とまったく同じ式になります。また、y の誤差の二乗和の項に対する回帰係数の項の重み λ を調整することで、λ = 0 のときに OLS とまったく同じ式になります。
このように、EN には OLS, RR, LASSO が3つともすべて含まれており、α と λ によって調整可能です。これだけ聞くと、EN だけあれば、OLS, RR, LASSO はやらなくても問題ないように思えます。
ここで注意することは、α と λ の決め方です。一般的にはクロスバリデーションとグリッドサーチを組み合わせた方法で α と λ を決めます。具体的には、α と λ の値の候補をそれぞれ準備しておき、それらのすべての組み合わせでクロスバリデーションにより y の推定を行い、推定結果が最も良い α と λ の組み合わせを選択します。

クロスバリデーションで推定性能を評価できるとはいえ、万能ではありません。クロスバリデーションの結果次第では、トレーニングデータにオーバーフィットしたような α と λ が選択される可能性もあります。
α と λ の設定に失敗すれば、EN により構築されたモデルの予測精度が低くなってしまいます。このような危険があるため、OLS, RR, LASSO も EN と並行して比較検討するとよいでしょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


