分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子や合成条件・製造条件・プロセス条件やプロセス変数などの特徴量 x と物性・活性・特性などの目的変数 y との間で数理モデル y = f(x) を構築したり、モデルに x の値を入力して y の値を予測したり、y の目標値を達成しうる x の値を設計したりします。このようなデータ解析・機械学習をする上で重要なことは、適切なモデルを構築することです。モデルの適用範囲 (Applicability Domain, AD ) が広いことを含めた予測性能が高いモデルを構築することが望まれます。
モデルを構築するとき、いろいろな手法 (回帰分析手法やクラス分類手法) があります。例えば回帰分析手法の例を挙げると、線形手法として OLS, PLS, リッジ回帰、LASSO, elastic net, SVR(線形カーネル), GPR (線形カーネル) など、非線形手法として SVR(ガウシアンカーネル), 決定木、ランダムフォレスト、ディープニューラルネットワークなどがあります。

今あるデータセット、特徴量 x、目的変数 y に合うモデル構築手法を選択することになります。一般的には、トレーニングデータとテストデータに分けて、トレーニングデータでモデルを構築してテストデータに対する予測精度を評価したり、ダブルクロスバリデーションで予測精度を評価したりします。


基本的には評価した結果が良好であった手法を使用することになります。ただ、AD の広さを考えたとき、x と y の関係が本質的に線形であれば、線形手法の方が AD は広くなります。そのため、x を設計して (特徴量エンジニアリングして)、例えば物理モデル・第一原理モデルによって y との関係が線形になるような x を作成して、x と y の間の関係を線形手法でモデル構築する方が AD は広くなります。
実際に y との間の非線形関係を x として表現して線形関係に持ち込むことで、その後のモデル構築において線形手法と非線形手法を比較すると、線形手法の方が AD が広がることは確認されています。
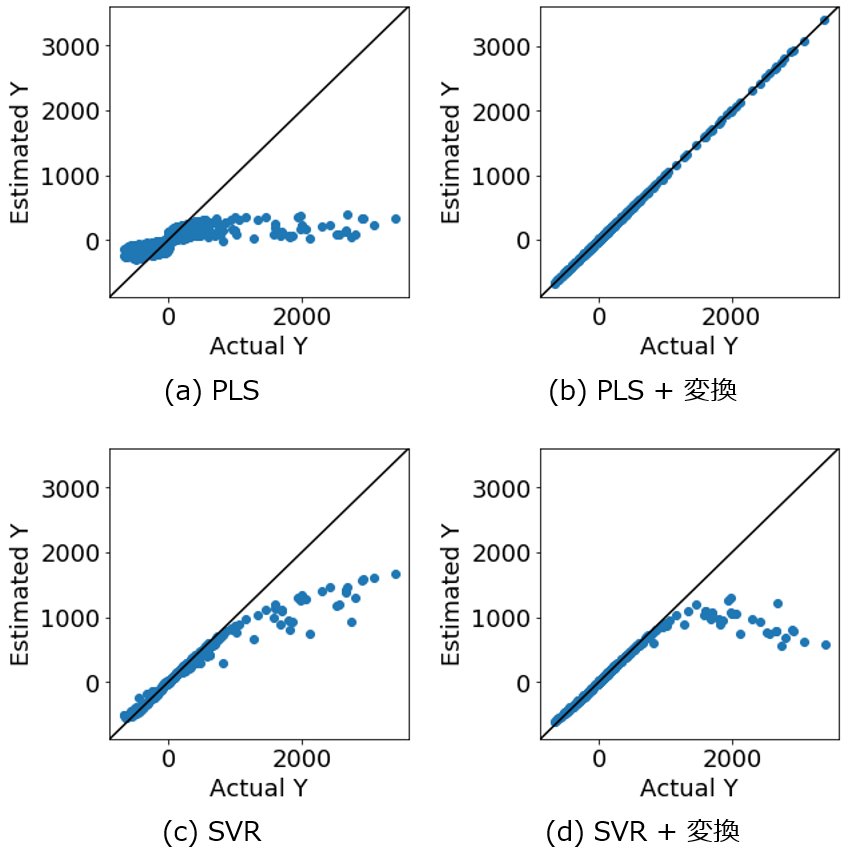
x と y の理論的な関係を求めることは難しいときもありますが、求めることができれば、それだけメリットがあります。ぜひチャレンジしていただければと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


