応化先生と生田さんがロバストなモデルについて話しています。
応化:今回は、ロバスト (robust) についてです。日本語に訳すと、頑健、ですね。
生田:ロバストも頑健も聞いたことがありません!
応化:日常生活ではあまり出てきませんよね。統計や機械学習をするとき、モデルを評価する言葉として出てきます。
生田:どんな意味ですか?褒め言葉ですか?
応化:はい、褒め言葉です。基本的には、ロバストなモデルを目指します。
生田:へー。回帰モデルとかクラス分類モデルとかにおいて、推定精度・推定性能の高いモデルを目指していました。推定性能が高いのと、ロバストなのとは違うんですか?
応化:広い意味では同じです。ただ、ロバストというのは、イレギュラーなことが起きたときでも推定性能が高い、って意味合いになります。
生田:イレギュラーなことって何ですか?
外れ値
応化:たとえば、外れ値です。
生田:あの、一つだけ他のデータと外れている値のことですか?
応化:そうです。下の図を見てみましょう。
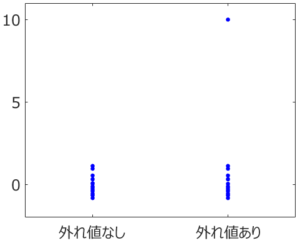
生田:右上の点が外れ値ですね。
応化:はい。左のデータセットには外れ値はありませんが、右のデータセットには外れ値があります。今、それぞれのデータ分布の中心を求めることを考えましょう。
生田:平均値ですね!
応化:では、それぞれのデータセットの平均値を見てみましょう。
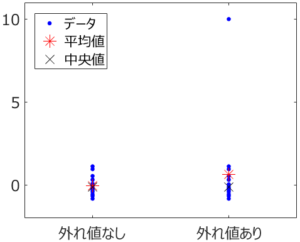
生田:あ、左の外れ値なしのデータセットにおける平均値と比べて、右の平均値は値が大きいですね。
応化:そうですね。右のデータセットは、平均値が1つの外れ値の影響を受け、大きくなってしまいます。このように、イレギュラーである外れ値があるかないかで値が変わってしまうのは、ロバストとはいえません。平均値は外れ値に対してロバストではないのです。
生田:平均値は外れ値に対してロバストではないのか!標準化 (オートスケーリング) とかでよく使ってたのに・・・。
応化:もちろん、外れ値がなければ平均値も問題ありません。ただ、平均値は外れ値の影響を受けやすいのが弱点です。
生田:わかりました。気をつけます。
応化:では、もう一度図を見てみましょう。中央値はどうなっていますか?
生田:外れ値なしのデータセットでも、外れ値ありのデータセットでも、同じような値です。
応化:そうですね。中央値は、平均値より外れ値の影響を受けにくいのです。つまり、中央値は平均値より外れ値に対してロバスト、といえます。
生田:中央値バンザイ!
応化:標準偏差は、平均値からの偏差でしたね。そういうこともあり、標準偏差も外れ値の影響を受けやすく、外れ値に対してロバストではないのです。
生田:え!じゃあどうすればよいのですか?
応化:平均値に対する中央値のように、標準偏差に対して中央絶対偏差があります。中央絶対偏差は、標準偏差より外れ値に対してロバストです。
生田:どのように中央絶対偏差を計算するんですか?
応化:すべてのデータから中央値を引き、すべて絶対値を取り、それらの中央値が、中央絶対偏差です。ただ、標準偏差のかわりに使うときは、中央絶対偏差に1.4826をかけて補正する必要があります。
生田:わかりました!平均値のかわりに中央値を使って、標準偏差のかわりに中央絶対偏差の1.4826倍を使えば、外れ値に対してロバストな標準化 (オートスケーリング) ができるってことですね。

応化:その通りです!ちなみに、そのようなロバストな標準化を行った後の主成分分析 (Principal Component Analysis, PCA) をロバスト主成分分析 (Robust PCA, RPCA)、部分的最小二乗法 (Partial Least Squares, PLS) をロバストPLS (Robust PLS, RPLS) とよんだりします。

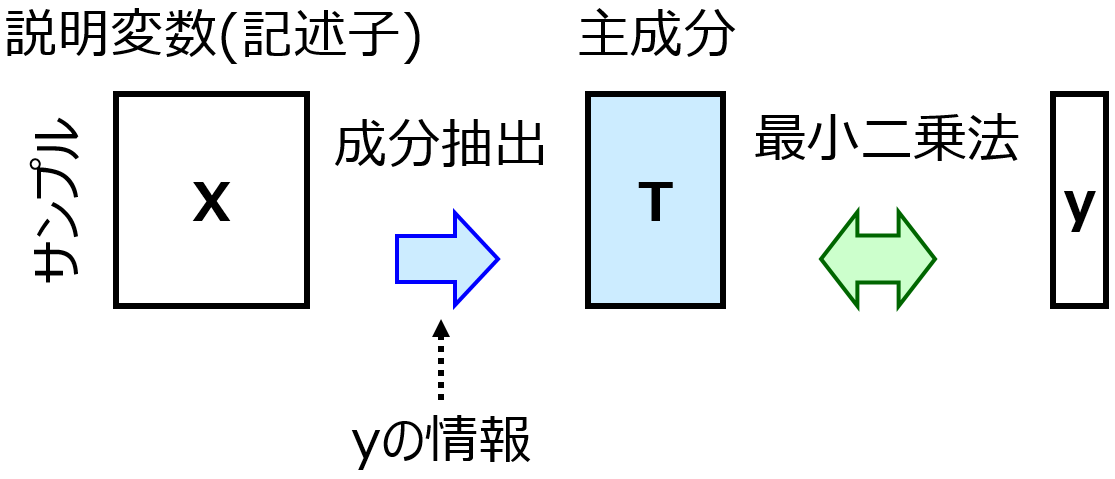
生田:へー。外れ値がありそうなときは、ロバストな標準化やRPCA・RPLS を使ってみます!
ノイズ
応化:もう一つのイレギュラーなことは、ノイズです。
生田:ノイズがあるときでもないときでも推定性能が高いのが、ロバストってことですか?
応化:そういうことです。下の図を見てみましょう。
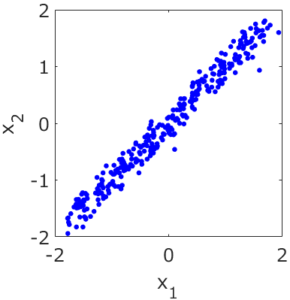
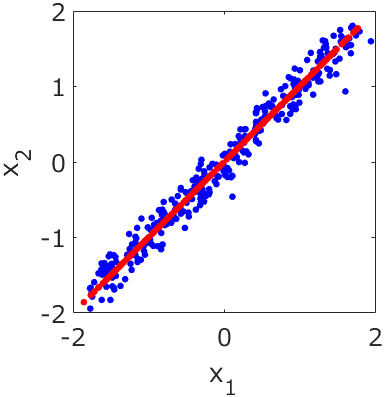
生田:2つの変数のデータですね。変数間には相関があります。
応化:今、2つの変数は同じ意味の変数であり、2つの変数の違いはノイズであるとしましょう。
生田:わかりました。対角線がノイズなしのデータってことですよね。対角線を引いて使いたいですね。
応化:主成分分析PCAならそれができます。PCAをした後に、第一主成分のみ使うと、データは下の図の赤点になります。
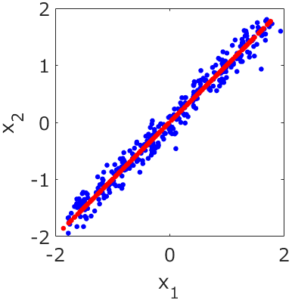
生田:対角線近くに点が並んでいますね。
応化:はい、この赤い点が、前処理としてPCAを使った後のデータ、ということになります。2変数の青点のデータにあったノイズが、取れていることがわかります。
生田:なるほど!
応化:PCAで前処理した後に、たとえば目的変数との間で回帰分析をすることで、ノイズの影響を受けにくい回帰モデル、つまりノイズに対してロバストなモデルができるのです。
生田:ノイズを含むデータがきても、一度赤点にしてから目的変数の値を推定するので、ノイズの影響が減るわけですね。
応化:その通りです!
生田:うまくPCAを使うとノイズに対してロバストなモデルを作れるんですね。外れ値のときに出てきたロバストな標準化と組み合わせればいい感じですね。
過学習 (オーバーフィッティング)
応化:過学習 (オーバーフィッティング) について覚えていますか?
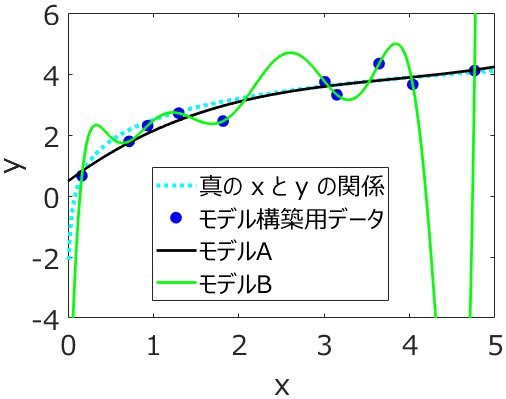
生田:はい!モデル構築用データ (トレーニングデータ) にモデルがより合うように過度に学習してしまうことですよね。
応化:過学習が起きたモデルは、ロバストなモデルではありません。
生田:そうか、過学習って、モデル構築用データのノイズにも合うように学習することですもんね。
応化:そうですね。過学習についても気をつけながら、外れ値やノイズなどイレギュラーなことが起きても推定性能の高いモデル、つまりロバストなモデルを目指しましょう。
生田:わかりました!
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。