分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
新しい x のサンプルを設計するとき、モデルの適用範囲 (Applicability Domain, AD) の中で y の予測値が望ましい値となる x のサンプルを設計できないとき、

特に y の目標が高いときには、ベイズ最適化で外挿を探索するのが有効です。

大量の x のサンプルを生成し、構築されたガウス過程回帰モデルを用いて x から y 予測値とその分散の値を計算し、それらを獲得関数の値を計算し、その値が最大となる x のサンプルを選択します。一度に1回実験・シミュレーションをする場合は、獲得関数の値が最大のサンプルや、獲得関数の値の大きい順に x のサンプルを並べたときに最初に来る実験・シミュレーションのしやすいサンプルを選択するのが一般的です。実験・シミュレーションとベイズ最適化によるサンプル選択を繰り返して、y の目標に入るサンプルの設計を目指します。
一方で、一度に複数回実験・シミュレーションできる場合は、ベイズ最適化で複数の x のサンプルを選択することになります。こちらの記事に書いたように、
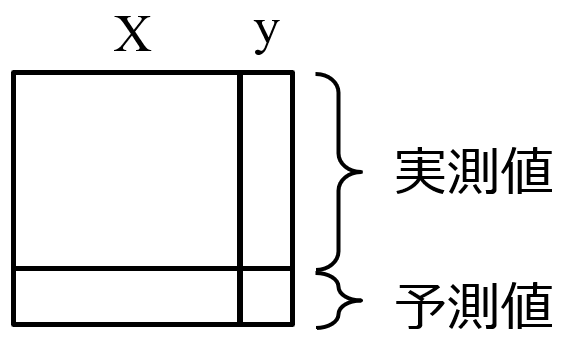
y の予測値をあたかも実測値のように考えて、モデルを更新しながら x のサンプルを選択する方法がありますし、また複雑なアルゴリズムにより複数回の実験をふまえた上で獲得関数の値が最大になるように選択する方法もありますが、実際の問題として、結果的に選択された複数のサンプルが類似してしまうこともあります。
このようなとき、x のサンプルのばらつきを明に考えて、ばらつくように複数個のサンプルを選択することがあります。
1つのやり方としては、ガウス過程回帰のカーネル関数の種類や、獲得関数の種類を変えて、x のサンプルを選択します。基本的に、カーネル関数はクロスバリデーションの予測結果がベストなものを一つ選択しますが、クロスバリデーションの結果がベストではないにせよ、良好な予測結果を出すものもあります。そのようなカーネル関数に変更すると、選択される x のサンプルも変わる傾向があります。また、獲得関数の種類を変えても、異なる傾向をもつ x のサンプルが選択されることがあります。このようにすることで、x のばらつきが生じ、色々な条件での次の実験・シミュレーションができるようになります。
もう1つのやり方としては、ベイズ最適化である程度の数、例えば 1000 サンプルほど獲得関数の値の大きい順に x のサンプルを選択した後に、その中で D 最適基準に基づく実験計画法により選択します。

こうすることで、獲得関数の値の大きい x のサンプル群の中から、なるべくばらつきが大きくなるように、複数のサンプルを選択できます。なおこのとき、何回か実験計画法の計算を繰り返し、結果的に選択されるサンプルの中に最も獲得関数の値が大きいサンプルが含まれるような結果を採用するとよいでしょう。
もちろん、獲得関数の値が大きい順に x のサンプルを並べ替えて、人の目で見て複数のサンプルを選択することもよいと思いますが、機械的に実施したいときには、上の2つの方法を検討してみるとよいでしょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。