新型コロナウイルスの影響もあり、セミナーや講演会はオンラインで行うようになってきました。対面でやるときも、オンラインでやるときも、だいたいどこでも聞かれる質問に、サンプル数をどれくらい増やせば十分ですか?いくつのサンプルを集めれば十分に予測精度の高いモデルができますか?、があります。みなさんは、サンプル数が大きくなると “モデルの予測精度” が上がることをイメージしており、下の図のように考えていると想像します。
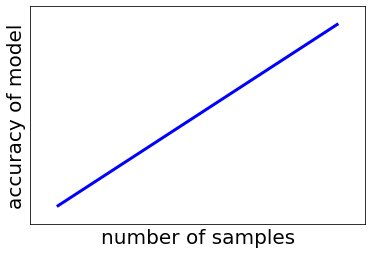
しかし、誤解を恐れずに言えば、上の質問における “モデルの予測精度” はサンプル数を増やしても変わりません。私の認識では、下の図のような感じです。
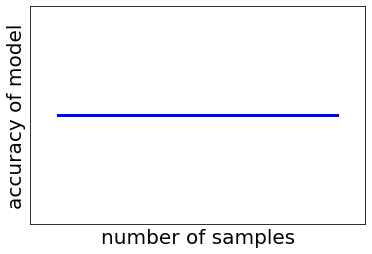
では、サンプル数が大きいと何が嬉しいかというと、同じくらいの誤差で予測できる新しいサンプルが多くなることです。別の言い方をすると、モデルの適用範囲 (Applicability Domain, AD) が広がるということです。

そのため、質問への回答としては、サンプル数が増えるということは、”モデルの予測精度” が上がるというより、新たに予測できるサンプル数が増えることを意味します、これにより設計しやすくなります、といったことになります。詳細についてはこちらをご覧ください。

”モデルの予測精度” の高いモデルは、何サンプルでもできるということです。ちなみに、どうしてもサンプル数の最小値が必要な場合は、とりあえず 30 サンプルくらいからはじめてはいかがでしょうか、とお答えしています。
ただ、サンプル数とモデルの予測精度の関係を、真に理解するためには、モデルの予測精度について解像度を上げて考える必要があります。
モデル、特に回帰モデルの目的は、今あるサンプル、例えば30サンプルについて、説明変数 X から目的変数 Y を再現性高く計算することではありません。目的は、今ないサンプル (新しいサンプル) において、X から Y を精度よく、つまり誤差小さく予測することです。もちろん、新しいサンプルは今ありませんので、Y の実測値はないため、どれくらいの誤差でそのサンプルを予測できるかはわかりません。今あるデータをうまく駆使して、新しいサンプルに対して、モデルがどの程度の誤差で予測できるか、見積もる必要があります。
新しいサンプル、と一言でいっても、色々なサンプルがあります。X の値が今あるサンプルとほとんど同じようなサンプルもあれば、今あるサンプルから X の値がかけ離れたサンプルもあります。どのようなサンプルでも、X の値があれば Y の値を予測できます。ただ、今考えているモデルがデータセットに基づくモデルである以上、どのサンプルを誤差小さく予測できるか、どのサンプルの誤差が大きくなってしまうかは、サンプルによって変わります。このあたりを議論するための概念が、AD です。

AD 内であれば Y の値を誤差小さく予測でき、AD 外であれば、誤差が大きくなる可能性が高いということです。
まとめると、モデルの性能を考える上で大事なことは、(今ない) 新しいサンプルをどのくらいの誤差で予測できるかであり、サンプルの誤差は、AD 内か AD 外かによって変わります。モデルの予測精度を議論するためには、サンプルの誤差だけでなく、AD を考慮する必要があるということです。モデルの予測精度は、Y の誤差と AD の広さがセットなのです。
たとえば、トレーニングデータで構築したモデルを、テストデータを予測することで検証することがあると思います。テストデータの r2, RMSE, MAE を確認したり、実測値 vs. 推定値プロットを見たりして、回帰分析手法を比較します。ここでは、基本的にトレーニングデータもテストデータも同じデータ分布からサンプリングされていることが前提ですので、どの回帰分析手法も AD の広さが同じである仮定のもと、モデルの予測精度を比較していることになります。そのため AD なしでも、テストデータの r2, RMSE, MAE が予測精度の指標と呼ばれたり、予測精度を実測値 vs. 推定値プロットで検証するといったりします。
回帰分析手法を比較するときは、AD を固定した、Y の誤差だけを見たモデルの予測精度で十分かもしれません。ただ、サンプル数が増える前後のモデルの予測精度を議論するときは、Y の誤差だけでなく、AD の広さも考慮する必要があります。そして、基本的にサンプル数が増えることで、Y の誤差が小さくなるというわけではなく、AD が広がるという認識をもっています。
もちろん、回帰分析手法ごとに、モデルの予測精度を比較する際も、Y の誤差だけでなく AD を考慮することで、より詳細に (解像度を上げて) モデルの予測精度を議論できます。AD 内でどのくらい予測できたか、AD 外でどのくらい予測できたか、を比較するわけです。AD を定量的に求めて比較することもあります。実際、テストデータは基本的にトレーニングデータと同じデータ分布であることが前提ですが、テストデータのサンプルが AD 外であるため、予測誤差が大きくなった、という結果もあります。このあたりは注意が必要です。
モデルを構築するということは、Y = f(X) を作ることだけでなく、AD を決めることとセット、という認識でいるのがよいと思います。そしてモデルの予測精度を検証してモデルを評価するときは、Y の誤差だけでなく AD を考えるようにしましょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


