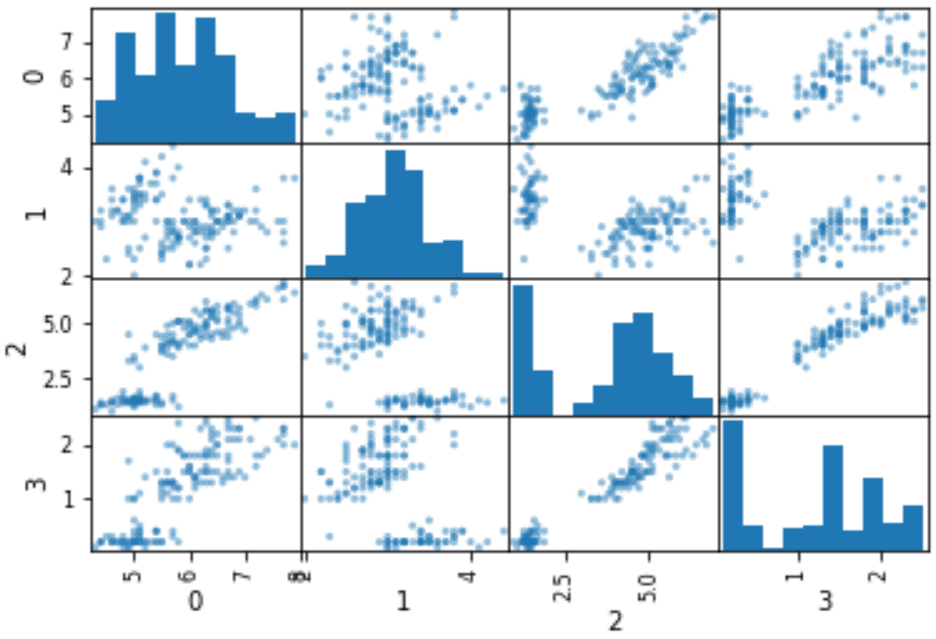
あまりたくさんの実験ができないとき、あまり多くの分析ができないとき、あまり繰り返しシミュレーションできないときのお話です。
今回は変数が複数 (多変量) のときです。ちなみに変数がひとつ (単変量) のときはこちらです。
サンプルが少ないときはどうするか？・・・うーん、仕方がないので幅で考えましょう！ (一変数・単変量で正規分布に従う場合)
あまりたくさんの実験ができないとき、あまり多くの分析ができないとき、あまり繰り返しシミュレーションできないときのお話です。データ数が少ないため、偶然の要素を排除できません。今回は一変数のときに、"偶然の要素を排除できない" とはどういうこと...
datachemeng.com
2018.11.25
多変量でも、データ数が少ないと偶然の要素を排除できません。今回は、少ないながらも手元にあるデータをつかって、データ分布を仮定します。具体的には、混合ガウスモデル (Gaussian Mixture Model, GMM) を仮定します。複数の正規分布の重ね合わせで表現される分布ですね。GMM について詳しく知りたい方はこちらをご覧ください。
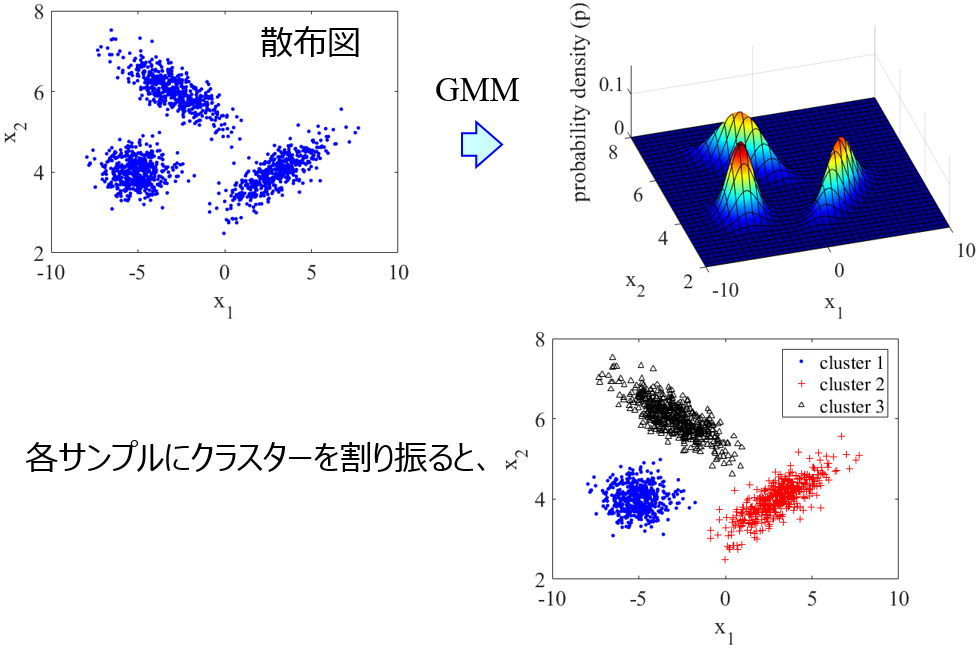
混合ガウスモデル (Gaussian Mixture Model, GMM)～クラスタリングするだけでなく、データセットの確率密度分布を得るにも重宝します～
クラスタリングについては、階層的クラスタリングと k-means クラスタリングをやりました。今回は、混合ガウスモデル (Gaussian Mixture Model, GMM) というクラスタリングの手法です。GMM を使うことで、データ...
datachemeng.com
2018.03.25
そして、仮定した分布に従うように、仮想サンプルをたくさん生成します。
今回も jupyter notebook でシミュレーションしながら、実行結果をご覧いただきながら説明します。お楽しみください！
ちなみに、回帰分析やクラス分類などの教師あり学習のときは、こちらの y-randomization で過学習 (オーバーフィッティング) しやすいデータセット・学習法なのか検証しましょう。
y-randomizationで過学習(オーバーフィッティング), Chance Correlation(偶然の相関)の危険度を評価！
回帰モデル・クラス分類モデルの評価のなかで、yランダマイゼーション (y-randomization) についてです。y-scrambling と呼んだりもします。やることは簡単で、目的変数 y の値をサンプル間でシャッフルして、回帰モデル...
datachemeng.com
2018.10.06
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。
