回帰分析やクラス分類をするとき、大きな目的の一つは、新しいサンプルに対する推定性能が高いモデルを構築することです。なので、モデルを構築したとき、そのモデルの 新しいサンプルに対する推定性能を検証する必要があります。

今、いくつかのサンプル・データがあるとき、そのデータセットをモデル構築用データ (トレーニングデータ) とモデル検証用データ (テストデータ) に分けなければなりません。トレーニングデータとテストデータの定義については、こちらをご覧ください。

トレーニングデータ・バリデーションデータ・テストデータの定義について書いておきます。バリデーションデータとテストデータとを逆の意味に使う人もいますが、ここでは wikipedia に記載されている内容にあわせます。トレーニング、つまり学習...

つまり、回帰モデルやクラス分類モデルを構築するためのデータと、そのデータで構築されたモデルを検証するためのデータを分けるわけです。今回は、クロスバリデーションでハイパーパラメータを最適化することを想定し、バリデーションデータは用いない場合について考えます。

では、どのようにトレーニングデータとテストデータとを分ければよいでしょうか。適する分割方法は、最初のデータセットが時系列データかどうかで異なります。時系列データというのは、時間にそって測定・観測されたサンプルであり、その時間的順番に意味があるデータのことです。たとえば、毎日の株価データ、毎月の売上データ、プラントにおける温度・圧力などの測定データなどです。

時系列データではないとき

定量的構造物性相関 (Quantitative Structure-Property Relationship, QSPR)・定量的構造活性相関 (Quantitative Structure-Activity Relationship, QSPR) における化合物データや材料のデータなどを扱うときです。

トレーニングデータとテストデータとを分ける方法としては、

基本的にはランダムに分ければ OK！

です。ランダムにトレーニングデータを選び、残りをテストデータとしましょう。

トレーニングデータとテストデータとのサンプル数の比については、もちろんサンプル数やデータセットの状況によりますが、だいたい

トレーニングデータ：テストデータ = 2：1

になるくらいがよいです。そもそもトレーニングデータのサンプル数が十分にないと、安定的に回帰モデル・クラス分類モデルを構築できないため、トレーニングデータのサンプル数を多めにしておくわけです。

基本的には、トレーニングデータとテストデータについて、それぞれ偏りなくばらついたデータを選ぶことが大切です。回帰モデル・クラス分類モデルには、モデルの適用範囲・適用領域がありますので、トレーニングデータからかけ離れたサンプルを精度良く推定することはできません。テストデータで検証したいのは、トレーニングデータとそこそこ似たサンプルを、どれくらいの精度で推定できるか、なわけです。

上で述べた、ランダムにトレーニングデータとテストデータとを選ぶ方法なら、たまたま偏ることはほどんど起きないため、偏りなくばらつくトレーニングデータとテストデータを分けることができます。

ただ、より積極的に、トレーニングデータを万遍なくばらつかせてサンプルを選択する方法の一つに、Kennard-Stone (KS) アルゴリズム があります。KSアルゴリズムはとてもシンプルです。以下のアルゴリズムでトレーニングデータを選択します。

データセットの説明変数について、サンプルの平均を計算する
平均とのユークリッド距離が一番大きいサンプルを選択する
まだ選択されていない各サンプルにおいて、これまで選択されたすべてのサンプルとの間でユークリッド距離を計算する
3. の距離の最小値を、各サンプルの代表距離とする
代表距離が最も大きいサンプルを選択する
3.～5. を繰り返す

このKSアルゴリズムで選ばれたサンプルをトレーニングデータ、選ばれなかったサンプルをテストデータとするわけです。下の図のように、すべてのサンプルから万遍なくサンプルを選択することができます。

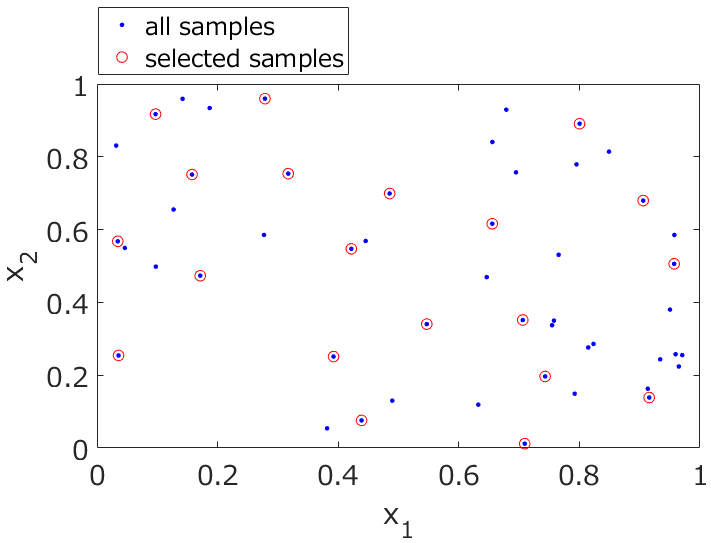
そして、

トレーニングデータ：選択されたサンプル
テストデータ：選択されなかったサンプル

とするわけです。

KSアルゴリズムを使ってみたい方は、こちらの DCEKit で、便利に KS アルゴリズムによるサンプル選択をご利用いただけます。

DCEKit (Data Chemical Engineering toolKit) を PyPI にリリース！

これまで化学データ・化学工学データのデータ解析に役立つツールや金子研で開発された手法に関する Python コードを Github にて公開してきました。このたびは、これらのツール・手法 (の一部) に加えて、新たな機能を追加して、DCEK...

時系列データのとき

時系列データの場合、ある時間に測定されたデータで構築されたモデルを用いて、その次の時刻のデータを推定・予測する必要があります。モデルを構築するとき、持っているデータはすべて過去のデータであり、構築したモデルを使って推定するのは、今もしくは未来のデータというわけです。モデルの推定性能の検証も、同じような状況で行ったほうが望ましいです。

ただ、データセットをランダムに分けてしまうと、未来のデータを使ってモデルを構築し、過去のデータを推定する、といったような状況が起きてしまいます。

そこで、トレーニングデータとテストデータを時間で区切り、より昔のデータをトレーニングデータとします。たとえば、2015年から2017年のデータがあるとき、