データ解析において、サンプル同士がどれくらい似ているか、サンプル間の類似度を調べるため、距離が用いられます。サンプル間の距離が小さい = ２つのサンプルは似ている、ということです。

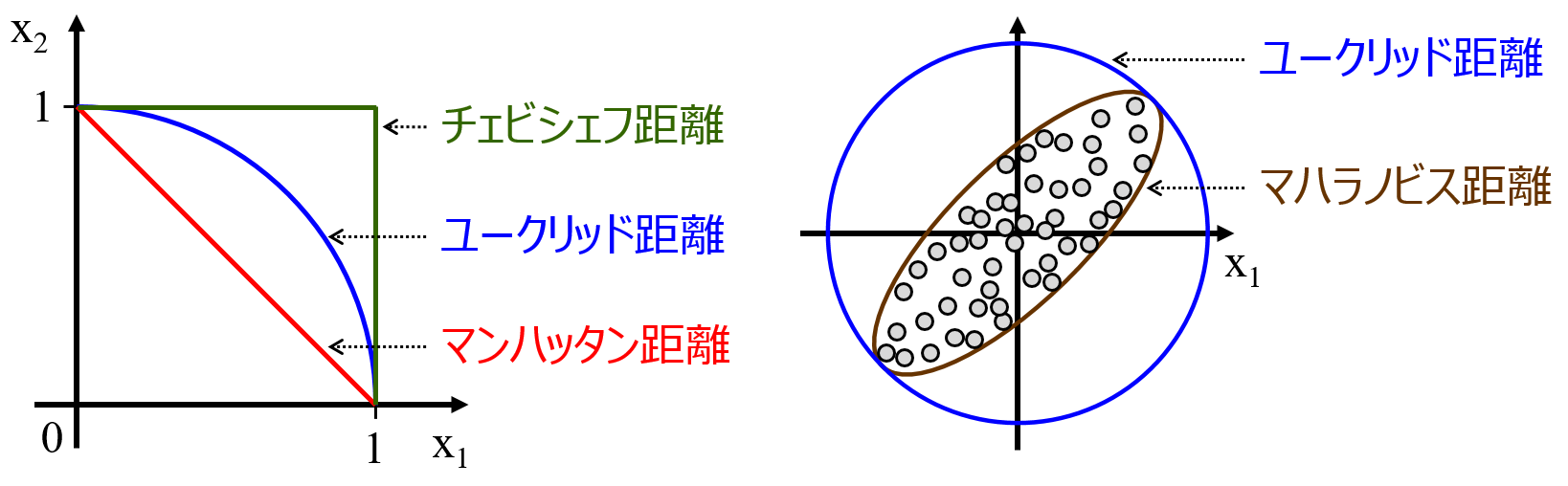
距離といってもいろいろあります。たとえば、ユークリッド距離・マンハッタン距離・チェビシェフ距離という距離がありますが、2つの変数 (記述子・特徴量など) x₁, x₂ のときに、原点からの距離が 1 となる集合は以下の図のようになり、距離ごとに異なることがわかります。

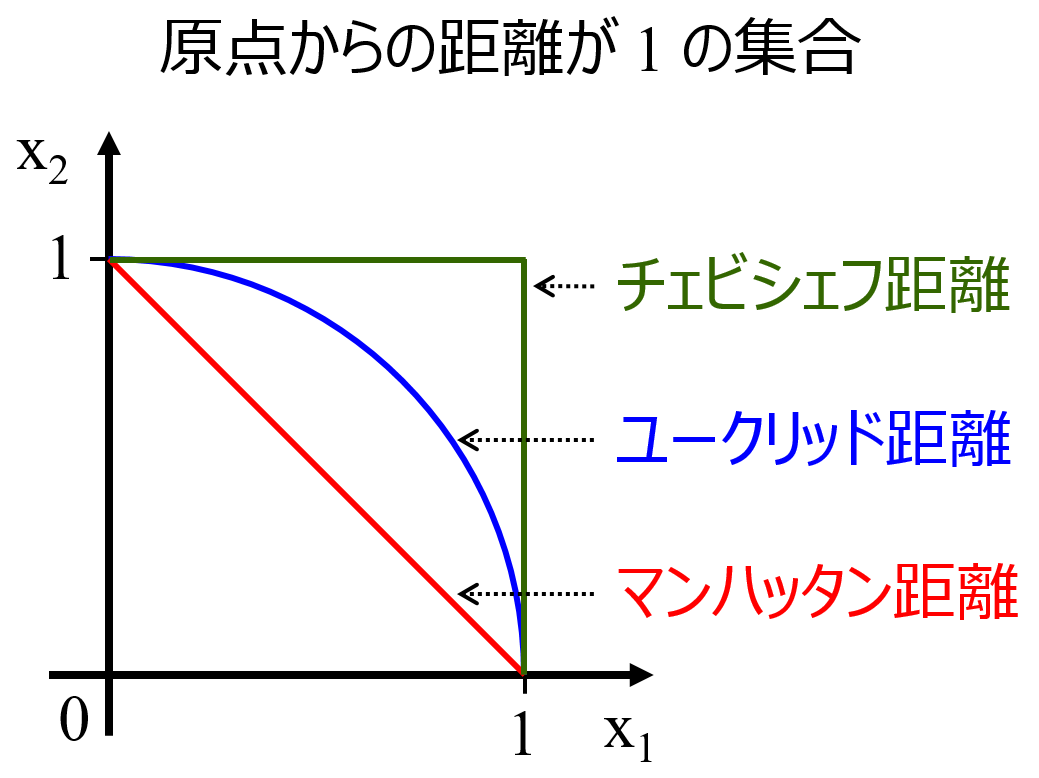
まずは、これらの三つの距離について説明します。

ユークリッド距離 (Euclidian distance)

最も一般的な距離はユークリッド距離でしょう。ユークリッド距離は、人が定規で測るような距離のことです。i 番目のサンプルと j 番目のサンプルとの間の距離 d_i_,j は以下の式のように計算されます。

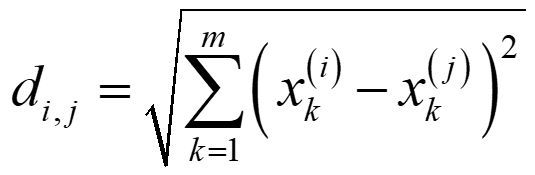
ここで m は変数の数、x_k⁽ⁱ⁾ は i 番目のサンプルにおける、k 番目の変数の値です。

特に理由がないときは、ユークリッド距離を使ってみるとよいでしょう。また、基本的には変数の標準化 (オートスケーリング) を行ってからユークリッド距離を計算しましょう。

マンハッタン距離 (Manhattan distance or City block distance)

マンハッタン距離は、碁盤の目のように区画された道しか通れない状況で測るような距離です。シティブロック距離とも呼ばれます。距離 d_i_,j は以下のように計算されます。

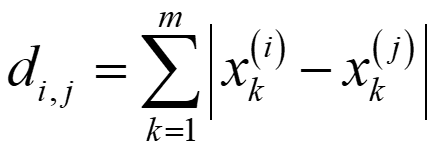
データセットにおいて、すべての変数が 0, 1 しか値を取らないダミー変数であるときは、マンハッタン距離を用いるとよいでしょう。ダミー変数の例としては、化学構造の場合のフィンガープリント (fingerprint) です。

例えば、(0, 0) と、(1, 0) や (0, 1) との間の距離は、ユークリッド距離でもマンハッタン距離でも 1 になりますが、(0, 0) と (1, 1) との間のユークリッド距離・マンハッタン距離は、それぞれ 2^0.5, 2 となり、(0, 0) と、(1, 0) や (0, 1) との距離の 2 倍離れている計算されるマンハッタン距離のほうが、ダミー変数の場合は妥当と考えられます。

チェビシェフ距離 (Chebyshev distance)

チェビシェフ距離では、各変数の値の差について、絶対値の最大値を距離とします。距離 d_i_,j は以下のように計算されます。

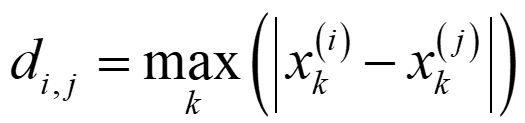
データセットに、重要でないノイズのような変数も含まれており、ノイズの影響を抑えたいときには、チェビシェフ距離を用いるとよいでしょう。各変数の値の差について、絶対値が最大にならない差は、考慮されないためです。

例えば、(0, 0) と、(1, 0) や (0, 1) との間の距離は、ユークリッド距離でもチェビシェフ距離でも 1 になりますが、(0, 0) と (0.1, 1) との間のユークリッド距離・チェビシェフ距離は、それぞれ 1.005, 1 となり、0.1 が誤差とみなされるときには、それを考慮しないチェビシェフ距離のほうが妥当と考えられます。ただの思いつきですが、(ノイズを含むことが多い) スペクトル間の距離では、チェビシェフ距離を用いるのが適切なときがあるかもしれません。

マハラノビス距離 (Mahalanobis distance)

マハラノビス距離は変数間の相関関係が (正でも負でも) 強いときに有効な距離です。変数間の相関関係を考慮しながら距離が計算されるため、下の図のように、2つの変数 x₁, x₂ に相関のあるデータセットの場合は、原点からの距離が同じ集合が楕円状になります。

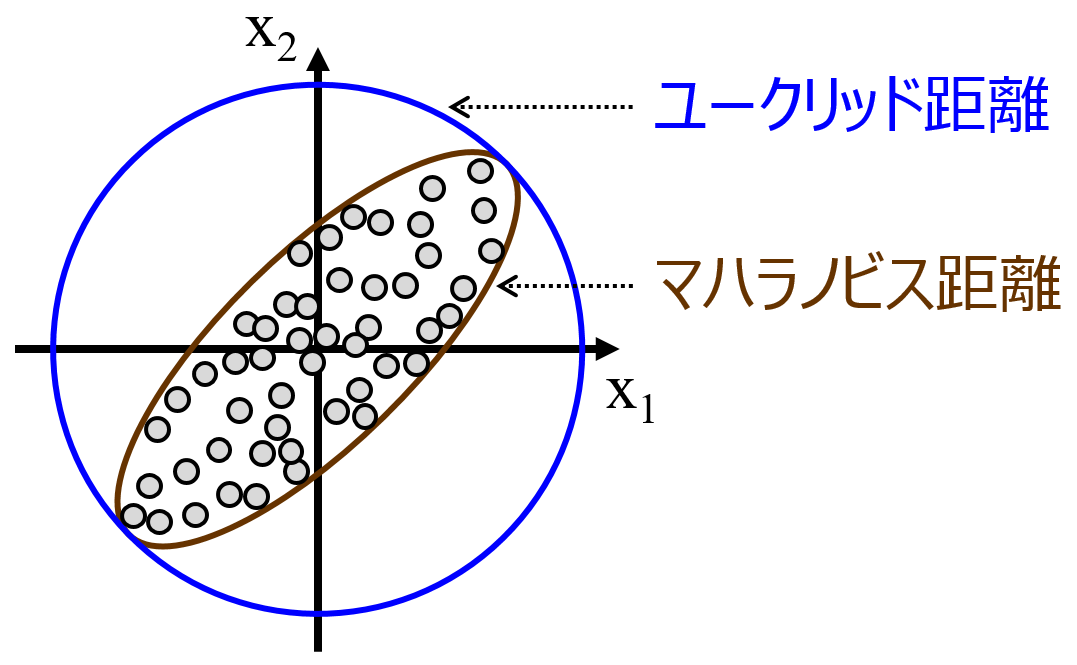
データセットにおける相関関係が考慮されることからもわかるとおり、マハラノビス距離はデータセットに依存します。サンプルが増えたり減ったりするなどしてデータセットが変わると、２つのサンプル間のマハラノビス距離は変わります。

距離 d_i_,j は以下の式のように計算されます。

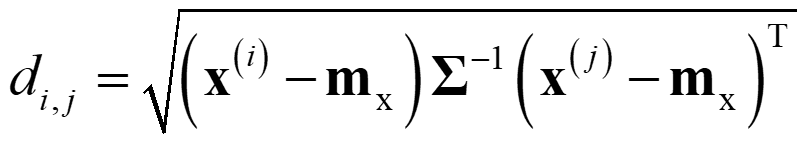
ここで x⁽ⁱ⁾, x^(j) はそれぞれ i 番目、j 番目のサンプルにおける変数の値が格納されたベクトル、m_x は各変数の平均値が格納されたベクトル、Σ^-1 は分散共分散行列 (対角線に各変数の分散、その他に i 番目、j 番目のすべての組み合わせの変数の共分散が格納された行列) です。基本的に変数の標準化をしていますので、m_x は考えなくてかまいません。すべての共分散が 0 (分散共分散が単位行列) であれば、マハラノビス距離はユークリッド距離と全く同じです。