今回は、説明変数・記述子・特徴量・入力変数を非線形関数で変換するお話です。
説明変数 X と目的変数 y との間で回帰モデルを作るとき、X と y との間に非線形の関係 (y = x12 + log(x2) とか) があるとき、一つのアプローチは 非線形の回帰モデルを構築することです。非線形の回帰分析手法として、Support Vector Regression (SVR)・ランダムフォレスト (Random Forest, RF)・ディープラーニングなどがあります。

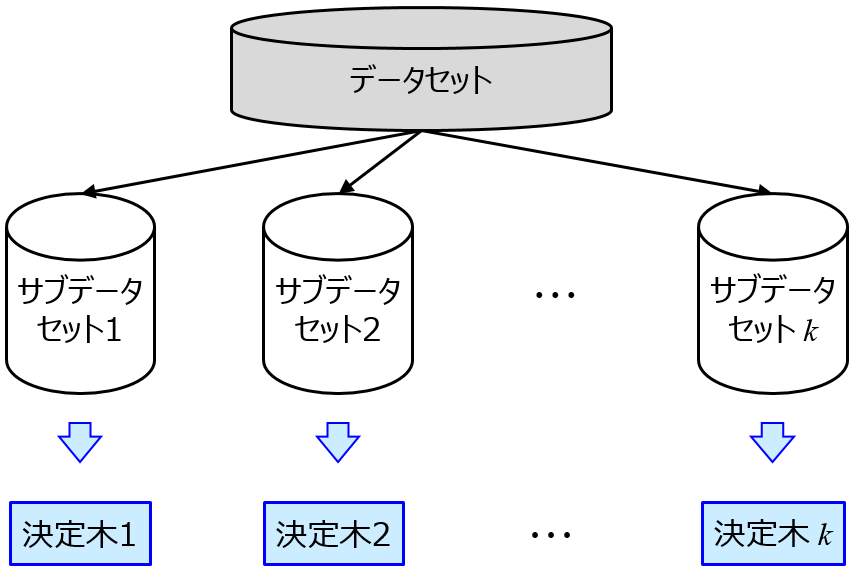
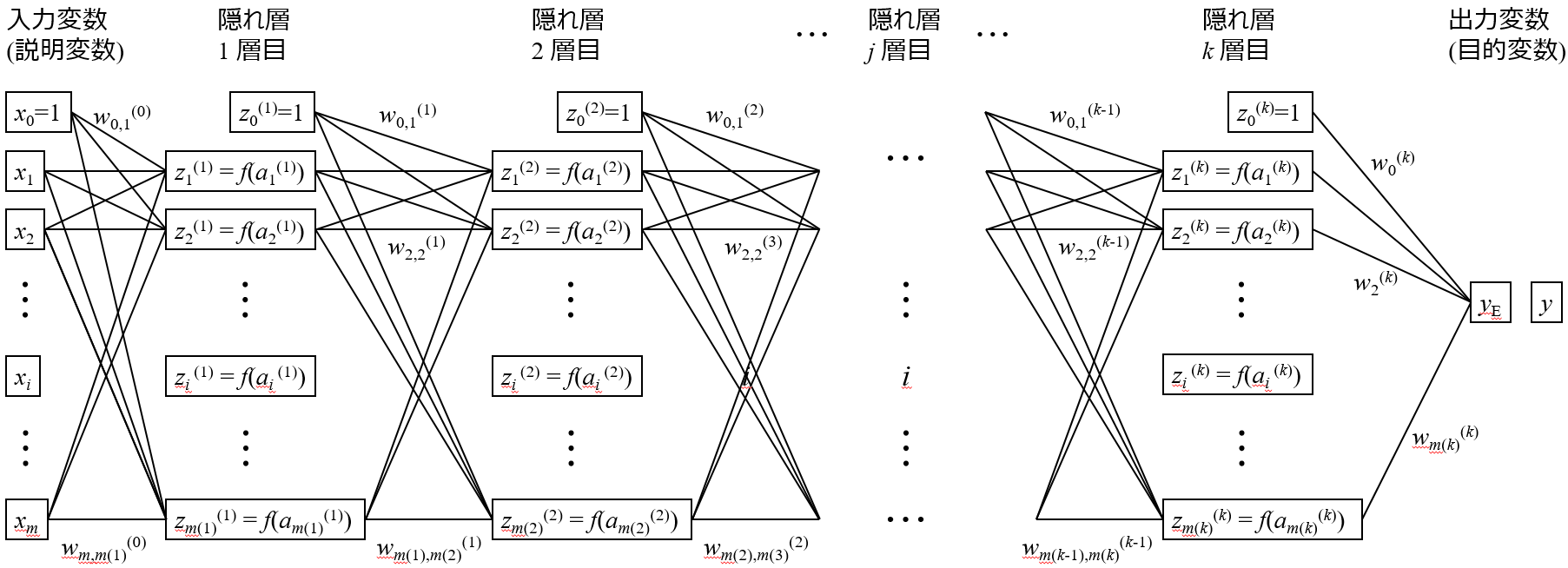
非線形手法で、X と y との間の非線形関係をモデル化するわけです。
非線形関係に対応するもう一つのアプローチとして、X を非線形関数で変換して、それを新たな X として用いる方法があります。たとえば、y = 5x12 + 7log(x2) のとき、x1 を x12 に、x2 を log(x2) に変換します。そうすれば、y と x12, log(x2) との間で回帰モデルを作るとき、線形の手法で OK! となるわけです。
もちろん X を正しく非線形変換するのが難しいのですが、、、今回は、2つの X と y との間の非線形性に対応する2つの方法
- 非線形の回帰分析手法を用いる
- X を非線形関数で適切に変換する
について考えてみます。
1. でも 2. でも、与えられたデータにおける X と y との間の非線形性には対応できそうです。1. について、特に SVR のような柔軟に対応できる手法では、X・y間のいろいろな非線形関係に対応できます。ただ、非線形回帰モデルによってモデル化された X と y との間の非線形性と、実際の非線形性とが一致するとは限りません。データに基づいて計算された非線形性ですので、それが一般的に正しいかどうかはわかりません。与えられたトレーニングデータ内では正しい、というだけなのです。
実際の非線形性と回帰モデルの非線形性が異なるとき、どんな問題が生じるでしょうか。
それは、
モデルが外挿をできにくくなる
という問題です。トレーニングデータ内では正しい非線形性なので、その中のデータは適切に推定できるといえます。しかし、トレーニングデータの範囲を外れると、範囲外での本来の X・y 間の非線形性と、回帰モデルの非線形性とが異なるわけですから、推定誤差が大きくなってしまいます。
言い換えると、モデルの適用範囲・適用領域が狭くなる、ということです。モデルの適用範囲・適用領域については、こちらをご覧ください。

2. の方法ではどうでしょうか。X を適切に非線形変換できていれば、y との間は線形で表現できます。非線形関係をモデル化するよりは、線形関係をモデル化するほうが、難易度は低そうです。つまり、モデルが外挿しやすそう、と考えられます。モデルの適用範囲が広くなる、ということです。
では、X を非線形関数で適切に変換して線形の手法で回帰モデルを作ったとき、非線形の回帰分析手法で回帰モデルを作ったときと比べてモデルの適用範囲が広くなる、という仮説を、数値シミュレーションデータで検証してみます。以下の解析結果が得られる Python のコードをこちらにおいておきます。
今回は、Xを2変数、yを1変数として、次の関係が成り立つとします。
y = 3 exp(x1) + 2 x23
そして x1, x2 について、それぞれトレーニングデータと2種類のテストデータを、以下のように生成します。
- トレーニングデータ: -5 から 5 までの一様乱数
- テストデータ1(AD内のみ): -5 から 5 までの一様乱数
- テストデータ2(AD外含む): -7 から 7 までの一様乱数
ADは、Applicability Domain (モデルの適用範囲) のことです。テストデータ1では x1, x2 の範囲をトレーニグデータと同じにして (AD内のみ)、テストデータ2では、x1, x2 の範囲をトレーニグデータの外側を含むようにしています (AD外含む)。
トレーニングデータ、テストデータ1、テストデータ2はそれぞれ 500 サンプルです。
以下の4つの手法で比較を行いました。
- X と y との間で PLS (PLS)
- x1 → exp(x1), x2 → x23 と、正しく変換した後に PLS (PLS + 変換)
- X と y との間で SVR (SVR)
- x1 → exp(x1), x2 → x23 と変換した後に SVR (SVR + 変換)
PLS が Partial Least Squares であり線形の回帰分析手法、SVR が Support Vector Regression でありガウシアンカーネルを用いた非線形の回帰分析手法です。
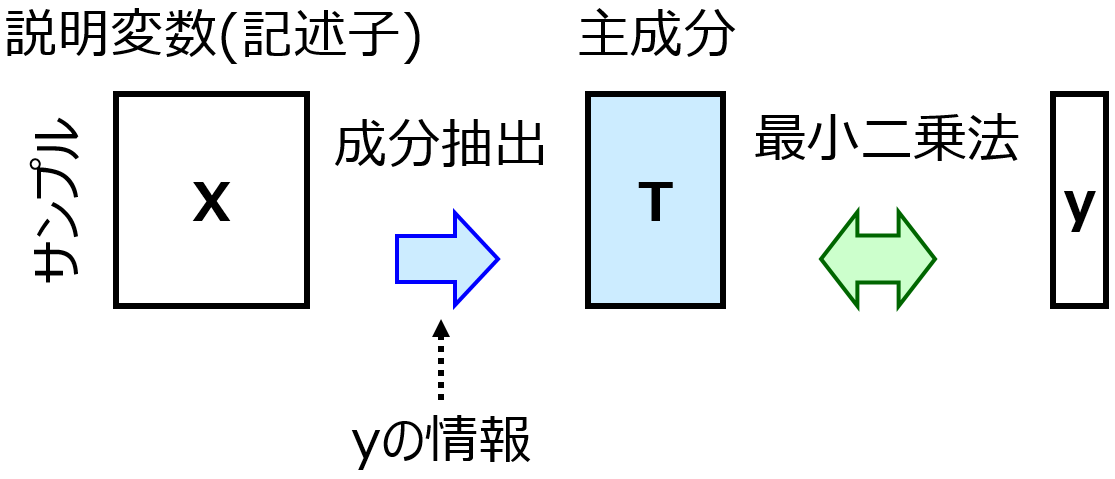

トレーニグデータを用いて、4つの手法それぞれで回帰モデルを構築し、テストデータ1(AD内のみ) を推定した結果は以下のとおりです。
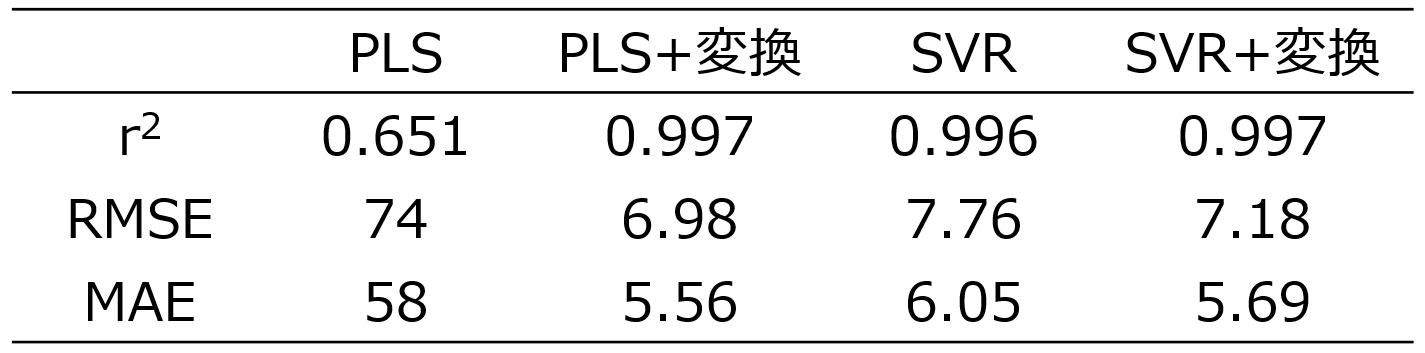
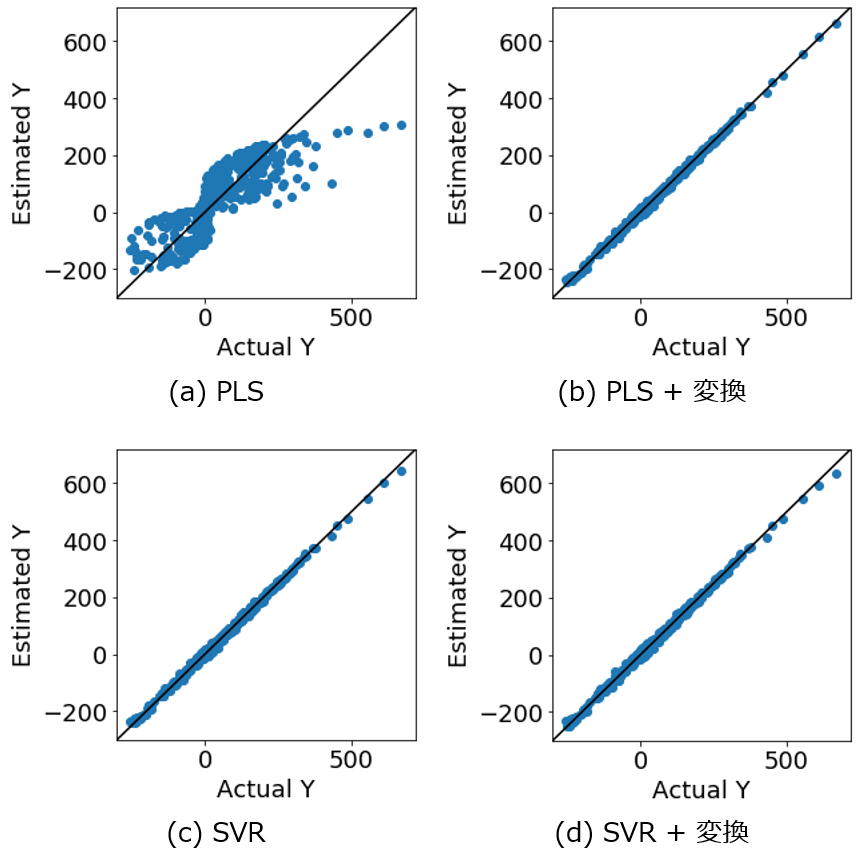
r2, RMSE, MAE についてはこちらをご覧ください。

X と y の間で直接 PLS を行ったときの推定結果は、他の結果と比較して r2 は小さく、RMSE, MAE は大きくなり、推定精度が低いことが分かります。y の実測値 vs. 推定値プロットを見ても、PLS 以外の3つの推定結果では、対角線付近にサンプルが固まっていて良好に y を推定できています。しかし、PLSでは対角線から離れたサンプルが多く、X と y との間の非線形性に対応できていません。他のX と y との関係は非線形なのに、線形の PLS を用いているため、当然といえば当然です。
ただ、他の3つの手法については大差ありませんでした。つまり X と y との関係が非線形のとき、非線形手法で回帰モデルを構築しようが、X を適切に非線形変換した後に回帰モデルを構築しようが、AD内の推定結果はほとんど同じ、ということです。
次に、テストデータ2(AD外含む) を推定した結果を見てみましょう。
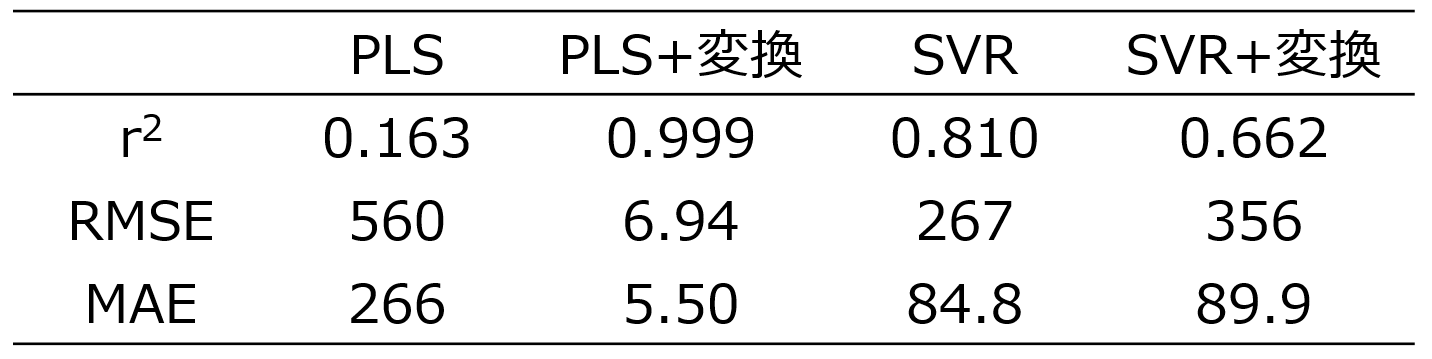
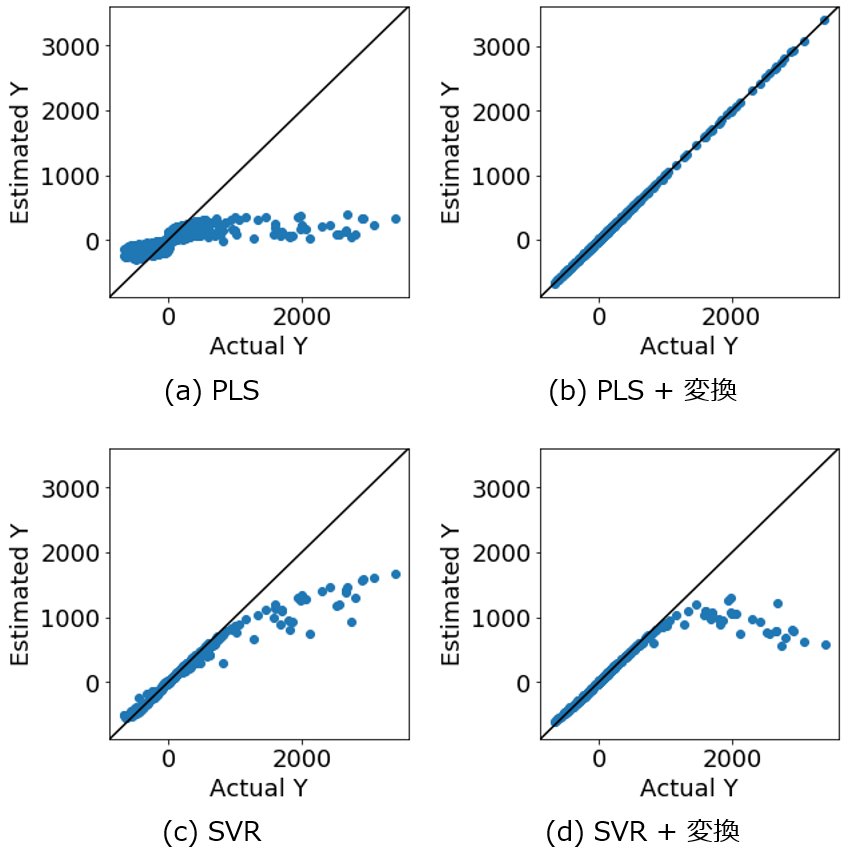
PLS の推定結果が、他の手法の推定結果と比較して、r2 は小さく誤差 (RMSE, MAE) は大きくなったのは、テストデータ1(AD内のみ) の推定結果と同じです。ただ今回は、SVR や SVR + 変換の推定結果が、PLS + 変換 と比べて悪くなっておりました。つまり、SVR や SVR + 変換 では、PLS + 変換と比較して、r2 は小さく RMSE, MAE は大きくなっています。
y の実測値 vs. 推定値プロットを見てみましょう。PLS で X と y との間の非線形性に対応できていないことは一目瞭然です。非線形の回帰分析手法である SVR を用いた場合でも、特に y が大きいときに、推定誤差が大きい結果でした。AD外のサンプルを推定できていないことが分かります。一方、PLS + 変換 を用いた場合、すべてのサンプルが対角線付近に固まっており、y 全体で良好な推定結果であることが分かります。X を適切に非線形変換した後に線形の回帰分析手法でモデル構築することで、非線形の回帰分析手法でモデル構築する場合と比較して、モデルの適用範囲が広がることを確認しました。
SVR + 変換 を用いた場合、y が大きいサンプルを正しく推定できていませんでした。推定誤差は SVR よりも大きい結果でした。X を正しく非線形変換したとしても、その後に非線形回帰分析手法を用いてしまうと、推定結果が悪くなることが示唆されました。
まとめと今後の課題
データ解析により、少なくとも上の数値シミュレーションデータにおいては、X を非線形関数で適切に変換して線形の手法で回帰モデルを作ったとき、非線形の回帰分析手法で回帰モデルを作ったときと比べてモデルの適用範囲が広くなる、という仮説を、検証できました。
もちろん、
- モデルの適用範囲が広くなるためには、(非線形変換後の) X と y との本来の線形関係をモデルで表現しなければならないが、特に X の変数が多いときや X 間の相関が高いときなど、正しく線形モデルを構築できるのか?
- そもそも、どうやって “X を非線形関数で適切に変換” するのか?
といった課題は残ります。
ちなみに、1. の課題についてはダブルクロスバリデーションによる変数選択およびモデル選択、2. の課題については いわゆる理論モデル・物理モデル・第一原理モデル、といった解決の方向性があると考えています。理論と統計の融合により、モデルの適用範囲が広がることで貢献できる可能性があることが示唆された、といった感じです。
ちなみにダブルクロスバリデーションについてはこちらをご覧ください。

以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。

