材料の活性・物性・特性は、化学構造だけで変化するものではなく、材料の作り方、つまり実験条件や製造条件によっても変化します。例えば高分子設計において、単量体 (モノマー) の化学構造だけでなく、そのモノマーの種類・組成比や、反応温度や反応時間といった重合条件によっても、高分子材料のさまざまな物性は変化します。実験条件・製造条件を X、材料の活性・物性・特性を Y として、X と Y との間で数値モデル Y=f(X) を構築することで、材料設計を効率化できます。
実験条件 X (モノマー1, 2, 3の組成・重合温度・重合温度) とその実験結果である材料物性 Y のデータセットがあれば、いろいろな手法により数値モデル Y=f(X) を構築できます。いろいろな手法についてはこちらをご覧ください。

データセットがなければ、最初に作成する必要があります。実験条件・製造条件のいくつかの候補を決め、それらの条件で実験をして材料物性を測定します。最初に実験する実験条件の候補を決める方法が実験計画法であり、詳しくはこちらをご覧ください。

モデル Y=f(X) を用いることで、まだ実験していない実験条件の候補の値をモデルに入力し、実験の結果としての材料サンプルがもつと考えられる物性の値を推定できます。推定値が材料物性の目標値になる、もしくは近いような実験条件の候補を選択することで、次に行う実験を決められます。
実験の結果が得られたら、それが目標を達成していれば終了です。目標を達成していなかったら、実験条件の候補と実験結果をあわせたものデータベースに追加して、再度モデルを構築します。新たに構築されたモデルを用いることで、次は別の実験条件の候補が選択されます。このように、モデル構築と次の実験の提案を繰り返すことを適応的実験計画法と呼びます。
これまで、Y の推定値が目標値に近いような候補を次の実験条件の候補として選択する、といった説明をしていました。しかし、Y の目標値と現状の Y の値との隔たりが大きく、適応的実験計画法、つまり実験とモデル構築とを繰り返すことで目標を達成することを目指す場合には、そのような Y の推定値に基づいた選び方よりも、「Y の目標を達成する確率」に基づいた選び方のほうが、実験回数が少なくて済む傾向があることが分かってきています。ベイズ最適化 (Bayesian Optimization, BO) です。
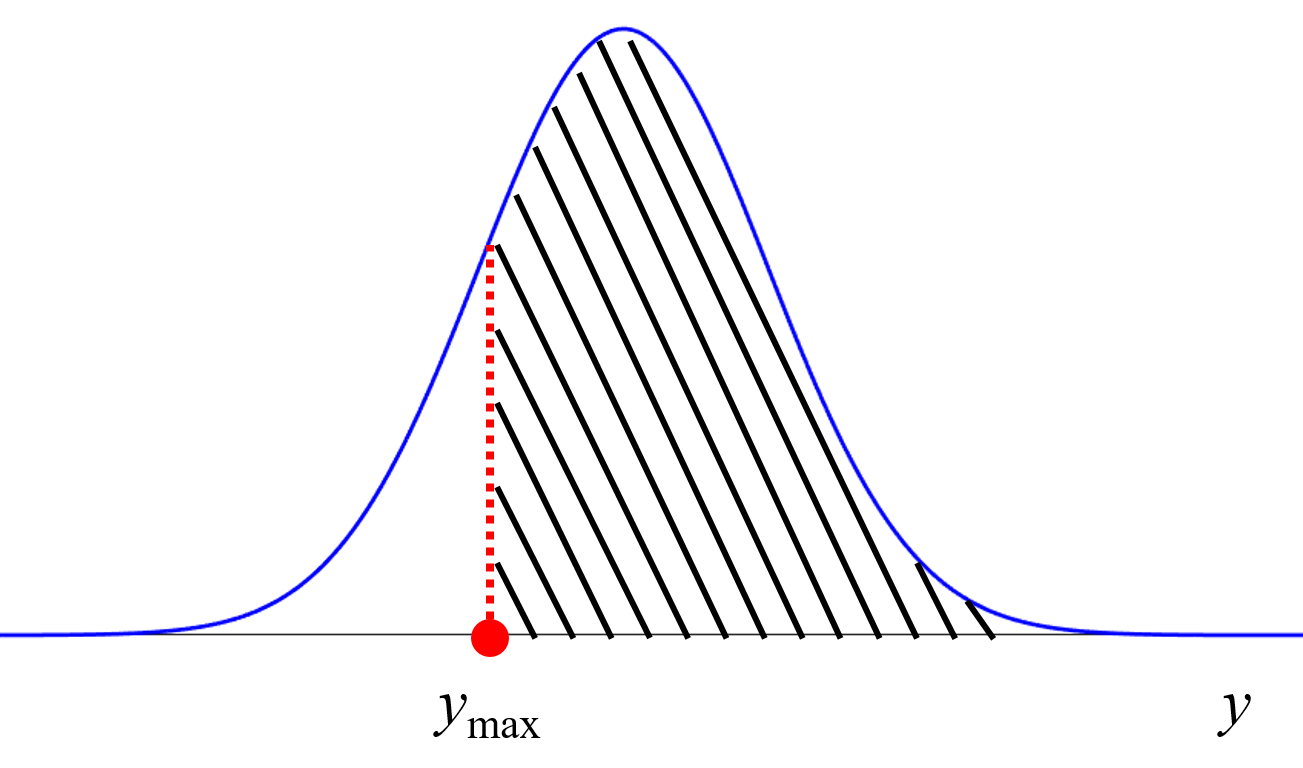

「Y の目標を達成する確率」について下図を用いて説明します。
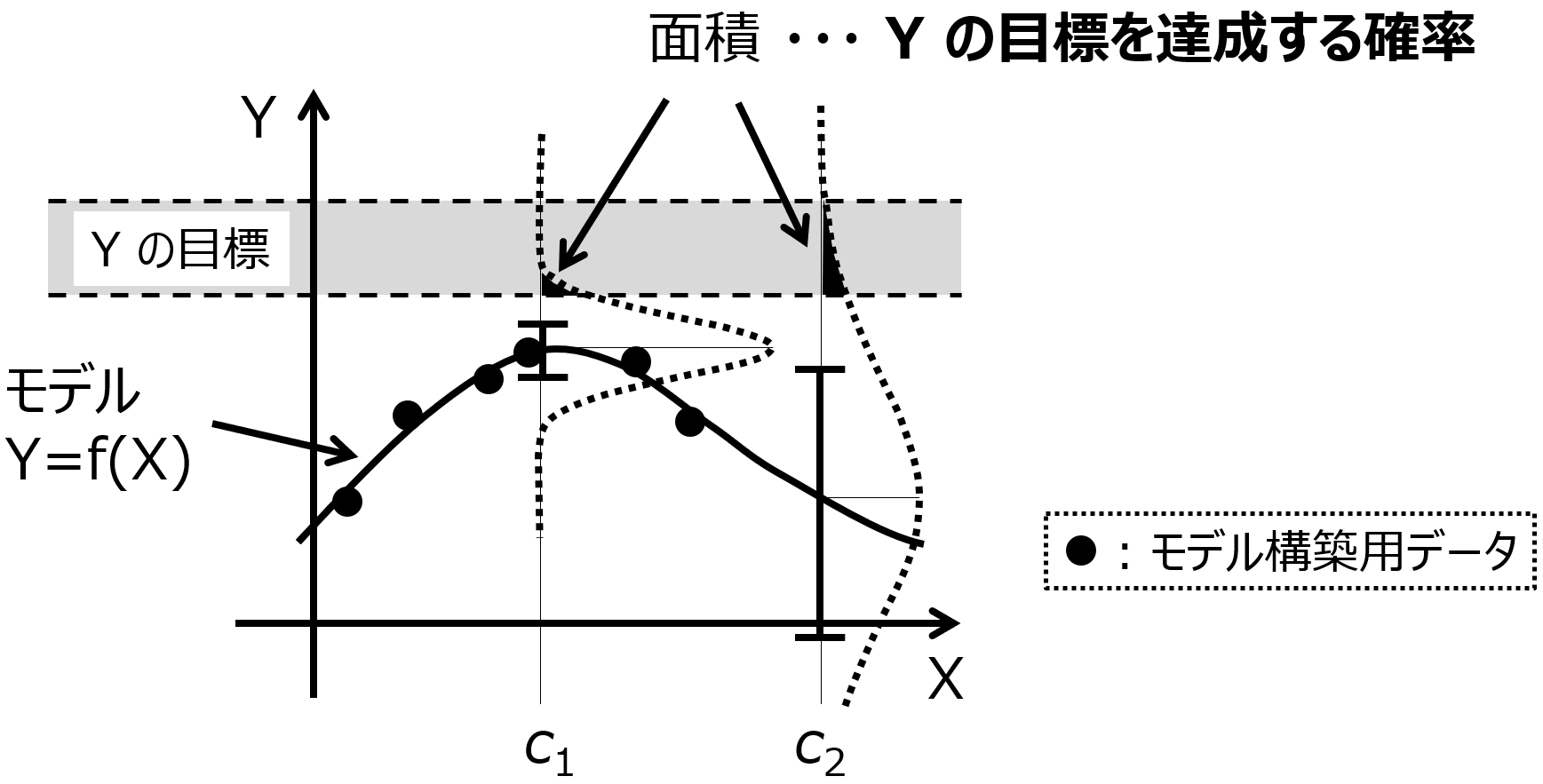
Y (縦軸) として 1 つの物性、X (横軸) として 1 つの実験条件 (特徴量) とします。図の黒点のデータベース (6 サンプル) を用いて、図中の曲線のモデル Y=f(X) が構築されたとします。モデルについて言いかえると、X にいろいろな値を入力したときの、Y の推定値の集まりが曲線ということです。
点線で囲まれたグレーの領域が Y の目標です。この範囲に入るような X の値を探索したい場合を考えます。単純に Y の推定値、つまり曲線だけに基づいて X の値を探すと、曲線が最も Y の目標に近づくのが、X の値が c1 のときになります。しかし、図を見ても分かるように、X が c1 の辺りにはサンプルがいくつも存在していて、これらのサンプルより Y の物性の値を向上させることは難しいと考えられます。
このような状況においても、Y の推定値がよいような X の候補を選ぶと、c1 となり、さらにはその次の実験条件の探索のときにも c1 付近の値となることが予想されます。物性の大きな向上が期待できない X の候補が選ばれ続けてしまい、毎回同じような実験をすることになってしまいます。そのため、c1 よりは既存のサンプルから離れたところの、(失敗するかもしれませんが) 少し挑戦的な X の値が選ばれた方が、まだよさそうです。図*** のように X の特徴量が 1 つであれば、もう c1 付近には有望そうな実験候補はないことが、目で見て分かりますが、例えば 10 個など複数の特徴量があると、状況がよく分かりません。
このような場合、Y の推定値だけでなく、推定値のばらつきを考えます。このばらつきは、ガウス過程回帰 (Gaussian Process Regression, GPR) やアンサンブル学習によって計算できます。


Y の推定値ごとに、推定値のばらつきも計算できたとします。上図の X の値が c1 における Y のエラーバーのようなイメージです。これにより、ある 1 つの X の値における Y の推定結果を、ばらつきを標準偏差、推定値を平均値とした正規分布として表せます。X の候補それぞれにおいて、正規分布で Y を推定できるわけです。
この正規分布は、確率密度関数 (Probability Density Function, PDF) ですので、ある範囲で積分すると、その範囲に入る確率として定義できます。つまり、Y の目標の範囲で積分する、つまり上図のように Y の目標の範囲で囲まれる正規分布の面積を求めることで、その面積の値を 「Y の目標を達成する確率」 と考えられるわけです。次の実験条件、つまり X の値の候補を選択するとき、推定値が物性値に近い候補ではなく、正規分布を Y の目標の範囲で積分した値である「Y の目標を達成する確率」が高い候補を選びます。上図においては、X の値が c1 のときより c2 のときほうが、面積が大きくなり、(推定値は目標から離れていても) c2 が選ばれることになります。
このような方法で次の実験条件の候補を選ぶことで、これまでのサンプルにおける物性の最良値と比べて、Y の目標が遠いときには、より外挿、つまりこれまでのサンプルにおける X の値から離れた候補が選ばれやすくなり、目標が近くなるにつれてより内挿が選ばれやすくなります。まだ Y の値が目標から遠いときには、挑戦的な実験条件が選択されるわけです。もちろん、目標に入る確率が高いといっても、確実にその目標に入るわけではありません。確率が高くなるような候補を選び、それを実験することを繰り返すことで、Y の推定値だけで候補を選択するよりも、より少ない実験回数で Y の目標に達成できる、という理論です。例えばシミュレーションや材料設計の課題において、ベイズ最適化により Y の推定値だけで候補を選ぶよりも少ない回数で、目標に達成できることが確認されています。
いくつか実験することは決まっていて、より少ない実験回数で目標達成したい場合にオススメです。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。