説明変数 X と目的変数 Y との間でモデル Y = f(X) を構築することがあります。Y が連続値の変数のときは回帰分析、Y がカテゴリー変数のときはクラス分類です。回帰分析、つまり Y が連続値の変数のとき、Y をカテゴリーの情報にすることでクラス分類に変換したり、クラス分類、つまり Y がカテゴリー変数のとき、Y を連続値にしたりすることもできます。
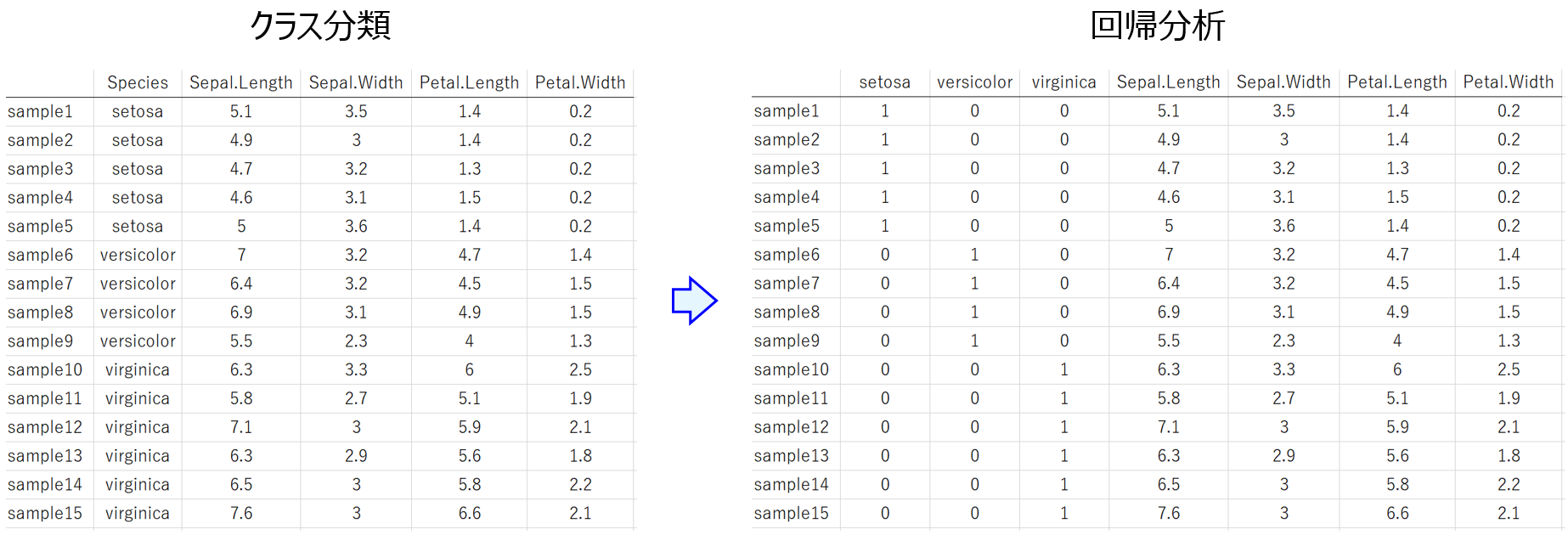
今回はそのあたりのメリット・デメリットについてお話しします。
まず、回帰分析からクラス分類に変換する場合です。たとえば、しきい値を決めて、しきい値以上のサンプルは 1 のクラス、しきい値未満のサンプルは -1 のクラスとすることで、Y を連続値からカテゴリーの情報に変換できます。このデメリットとしては、Y の情報量が小さくなることです。たとえば Y の値が -10 から 10 まで分散していて、しきい値を 0 にしたとき、Y が 0.1 だったサンプルも、5 だったサンプルも、10 だったサンプルも、1 のクラスになってしまいます。
Y の情報量が小さくなる一方で、以下のようなメリットもあります。
- オーバーフィッティングが起こりにくくなる
- モデル設計がしやすくなる
- クラス分類特有の手法が使えるようになる
多くの場合、Y はなんらかの測定値であり、測定誤差などのノイズがあります。各サンプルの Y の値を、1 や -1 として丸め込むことで、そのノイズを無視できます。モデリングの際のノイズが低減することで、オーバーフィッティングが起こりにくくなります。
また、回帰分析の手法と比べて、クラス分類の手法のほうがシンプルな場合が多く、モデルの設計がしやすいです。たとえば、ガウシアンカーネルを用いたサポートベクター回帰 (Support Vector Regression, SVR) と、同じくガウシアンカーネルを用いたサポートベクターマシン (Support Vector Machine, SVM) を比べたとき、

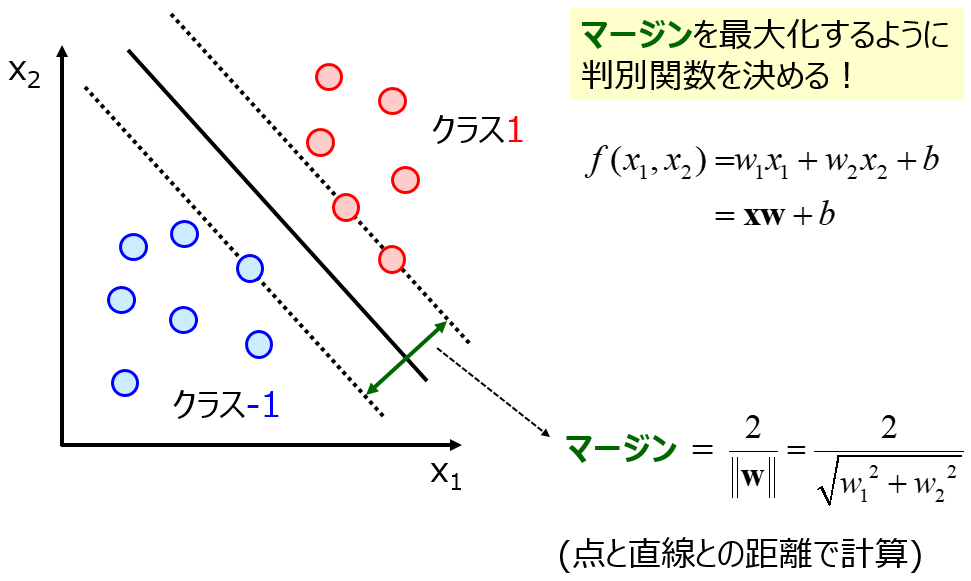
SVR にはハイパーパラメータが三つもありますが、SVM では二つです。SVR より SVM のほうがモデル設計をしやすいといえます。
あとは、クラス分類特有の手法が使えるのもメリットです。たとえば、半教師あり学習は回帰分析よりもクラス分類の方が、いろいろな手法があります。その理由の根底にあるのは、クラス分類であれば、Y のあるサンプル (ラベル付きサンプル) と類似した Y のないサンプル (ラベルなしサンプル) は、そのラベル付きサンプルと同じクラスである仮定は妥当な場合が多いですが、回帰分析において、ラベルなしサンプルの Y の実測値に関する情報はまったくない、ということです。たとえば回帰モデルにより Y の予測値を計算できますが、実測値と離れているかもしれませんし、離れていないかもしれません。

仮に、半教師あり学習に使用するラベルなしサンプルにおける、Y の予測値以上の有益な情報が得られるのであれば、学習に使用するのではなく、まさに Y の予測に使用するべきですね。
次に、クラス分類から回帰分析に変換する場合です。ただ、このときのメリット・デメリットは、基本的に上のの回帰分析をクラス分類にするときのメリット・デメリットの裏返しになります。デメリットとしては
- (Y の数が増えて) オーバーフィッティングが起こりやすくなる
- クラス分類特有の手法が使えなくなる
- モデル設計がしにくくなる
です。
一方メリットは、
- 回帰分析の手法が使えるようになる
- 情報量が大きくなる
です。たとえば、サンプルごとのクラス 1 らしさ、クラス -1 らしさのようなものも評価できるようになります。結果の確からしさを評価できるわけですね。もちろん SVM でも判別面からの距離という指標で評価できたり、アンサンブル学習でも各クラスの確率を評価できたりしますが、回帰分析により一般的に評価できるようになります。
扱う分子・材料などの (時系列) データ、そして研究テーマによって、デメリットよりもメリットの方が優位なときは、
- 回帰分析 → クラス分類
- クラス分類 → 回帰分析
の変換を検討してみるとよいかと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


