タイトルで言いたいことはほとんど言っていますが、丁寧に説明します。たとえば最小二乗法による線形重回帰分析や部分的最小二乗回帰 (Partial Least Squares Regression, PLS) や Least Absolute Shrinkage and Selection Operator (LASSO) などにおいて回帰係数が求められます。
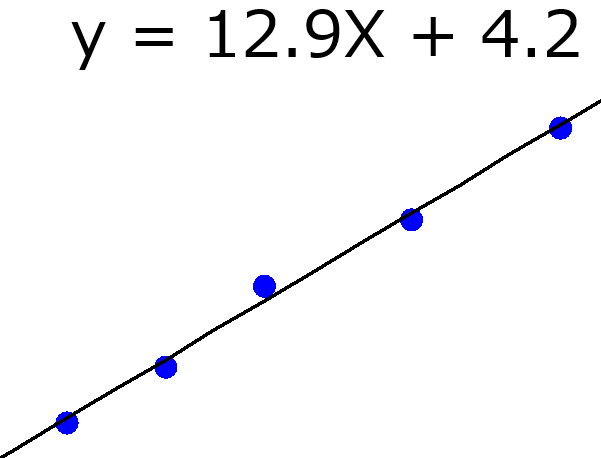
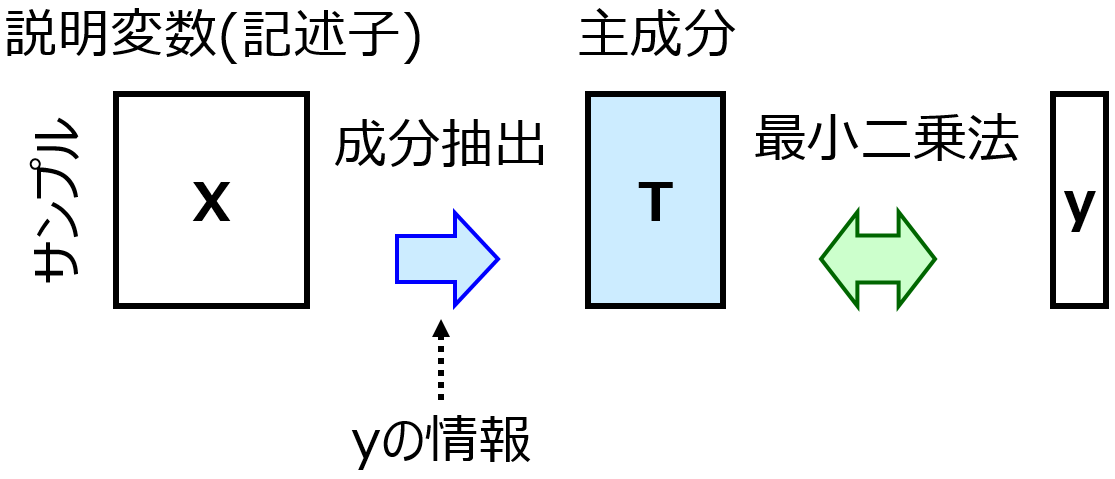
回帰係数は見ため的に、目的変数 Y に対する説明変数 X の寄与度のように見えます。各 X を 1 変化させたときに、Y がいくつ変化するか、といったものです。ただこれは、各 X を (他の X にまったく影響を与えず) 独立に変化させることができるとき、という大前提があります。いいかえれば、すべての X の間の相関係数が 0 のときしか、回帰係数は Y に対する X の寄与度とはいえません。しかし実際は、すべての相関係数が 0 になることは基本的にありえません。もちろん、主成分分析 (Principal Component Analysis, PCA) や PLS をしたあとの主成分を X とすれば、主成分間の相関係数はすべて 0 ですので、y に対する主成分の寄与度を求めることができます。しかし、実際に求めたいのは y に対する X の寄与度です。主成分の寄与度を用いるのであれば、そのそも主成分は何を意味するのか?、を別に議論する必要があります。
また、たとえば Y のサンプルが [2, 4, 6, 8] のデータセットに対して、2つの X があり、それぞれサンプルの値が [1, 2, 3, 4]、[2, 4, 6, 8] としたとき、回帰係数としては [2, 0] や [0, 1] や [1, 0.5] など、無限に候補が存在します。これは X 間の相関係数が 1 の極端なケースですが、相関係数が 1 (もしくは -1) に近いほど、同様の現象が起きます。
以上のことから、回避係数 = Y に対する X の寄与度、とすることは危険です。唯一、、回帰係数 = Y に対する X の寄与度とみなせるのは、主成分回帰や PLS で1つの主成分のみを用いて回帰係数を求めたときです。1成分モデルですので主成分に対応する回帰係数が 1 つ求められ、それをローディングと掛け算することで X の回帰係数に変換できます。これは Y に対する X の寄与度とすることができます。ただ一方で、1 成分しか用いませんので、多くの場合でモデルの予測精度は他のモデルと比べて低く、機能的であるとはいえません。あくまで、その予測精度の範囲内において、回帰係数を X の Y への寄与度とすることができます。
また、たとえば X の中に、Y = X2 のような関係の変数があるとき、X が正の値のときには Y に対して正の寄与がありますが、X が負の値のときには Y に対して負の寄与になります。線形モデルでは、このような値ごとの寄与の違いがあるときも、すべてまとめて、全体で一つの係数としてしまいます。そのため、データセット全体での Y と X の関係性を議論したいときは、線形モデルではなく非線形モデルで、正負も考慮した X の寄与度ではなく X の重要度で、議論します。たとえばランダムフォレストでは、X ごとに重要度を計算できます。
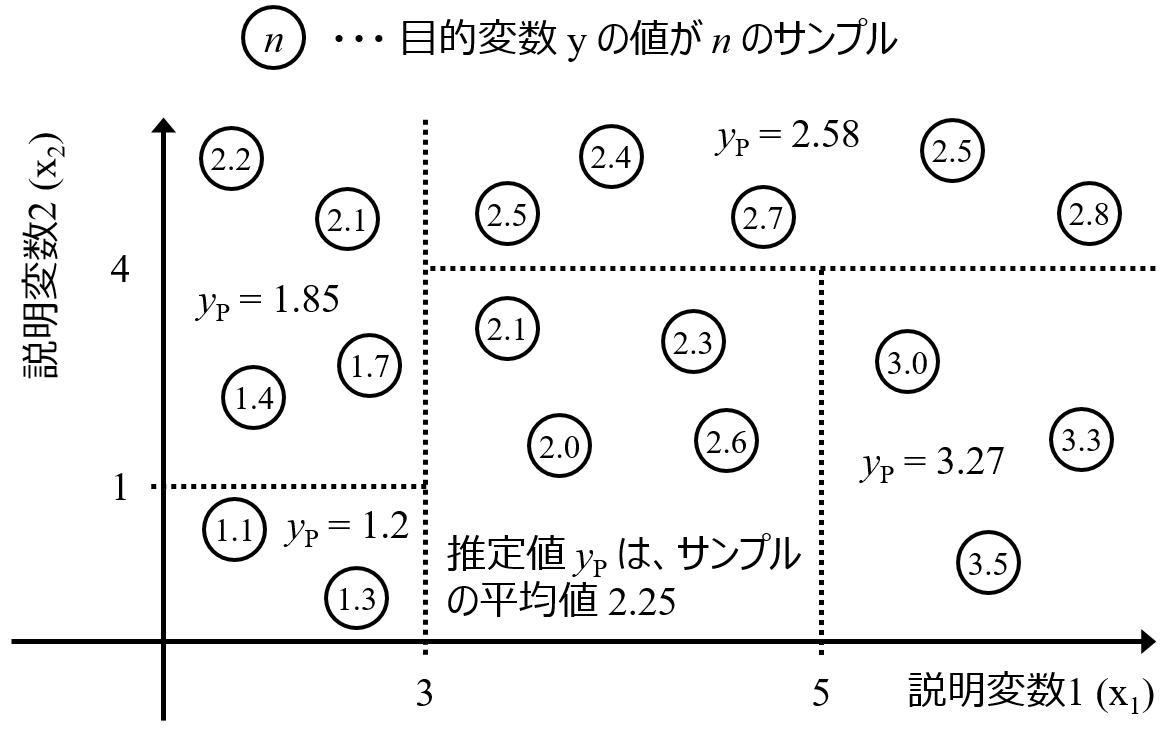
X が Y に対して正に寄与しているのか、負に寄与しているのかはわかりませんが (そもそも上述したように非線形の場合には、両方のときもあります)、他の変数と比較した重要度を議論できます。このように、データセット全体でモデルを解釈して、X と Y の間の関係性を議論したいときには、変数の重要度を用いるとよいでしょう。
非線形モデルにおける全体の関係性ではなく、局所的な関係性を議論するときは、こちらをご覧ください。

以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


