金子研の論文が Chemometrics and Intelligent Laboratory Systems に掲載されましたので、ご紹介します。タイトルは
Adaptive design of experiments based on Gaussian mixture regression
です。
Gaussian Mixture Regression (GMR) や Generative Topographic Mapping Regression (GTMR) では、説明変数 X から目的変数 Y (Y が複数でもOK!) を直接的に推定する、といった回帰モデルの直接的逆解析ができます。
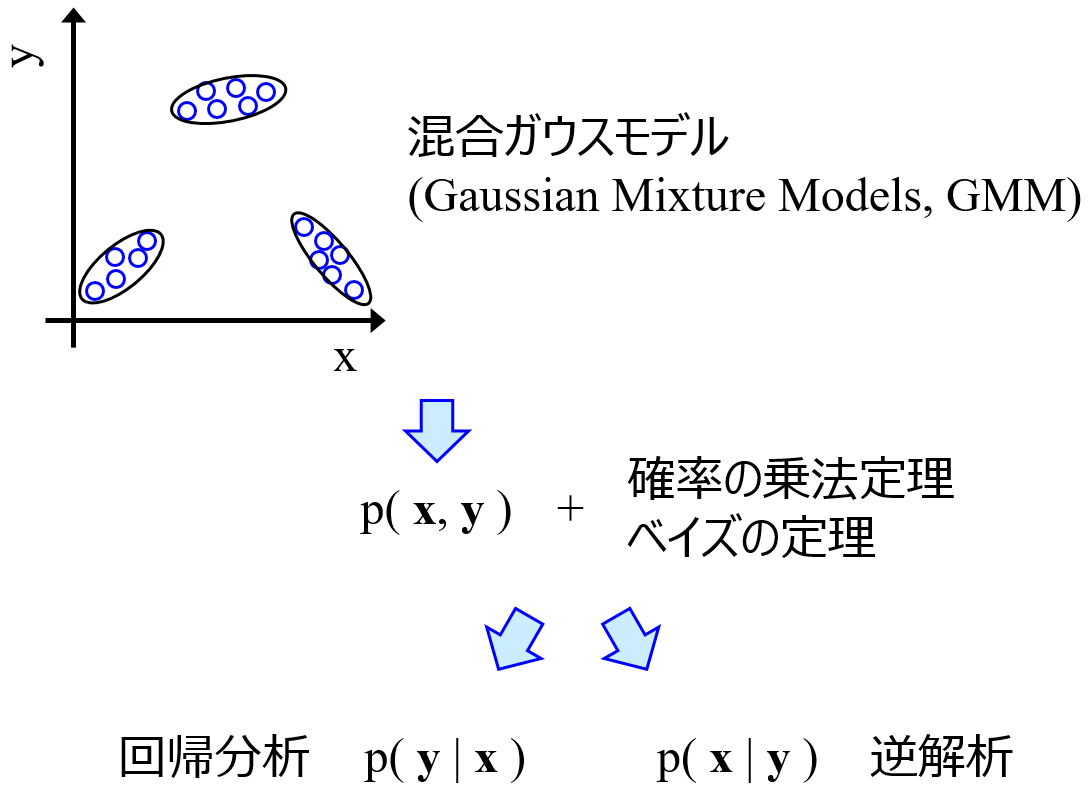

GMR による適応的実験計画法の大きな流れとしては、まず実験計画法で最初に実験する実験条件の候補を決めて、実際に実験したデータ (X と Y のデータセット) を用いて GMR によりモデルを構築します。そして、Y の目標値をモデルに入力し、直接的逆解析法により、次の実験条件の候補を推定します。この後は、推定された実験条件の候補での実際の実験、実験後のデータを用いた GMR モデルの再構築、次の実験条件の提案を繰り返します。
GMR では、ハイパーパラメータとして以下の3つがあります。
- 正規分布の数
- 分散共分散行列の種類
- mode で推定するか、mean で推定するか
論文では、データセットが更新されるごとに、すべての組み合わせでクロスバリデーションを行い、最適な組み合わせを選択しています。特に、mode で推定するか、mean で推定するかについて、これまでハイパーパラメータとして認識していなかったのですが、データセットによって適した方法が異なることが分かってきて、今回からハイパーパラメータとして最適化の対象としました。
論文ではシミュレーションによる検証ではありますが、複雑な非線形関数で実験条件 X と物性 Y の間の関係を仮定し、適応的実験計画法を実施しました。結果として、これまで良好な結果を達成していたベイズ最適化
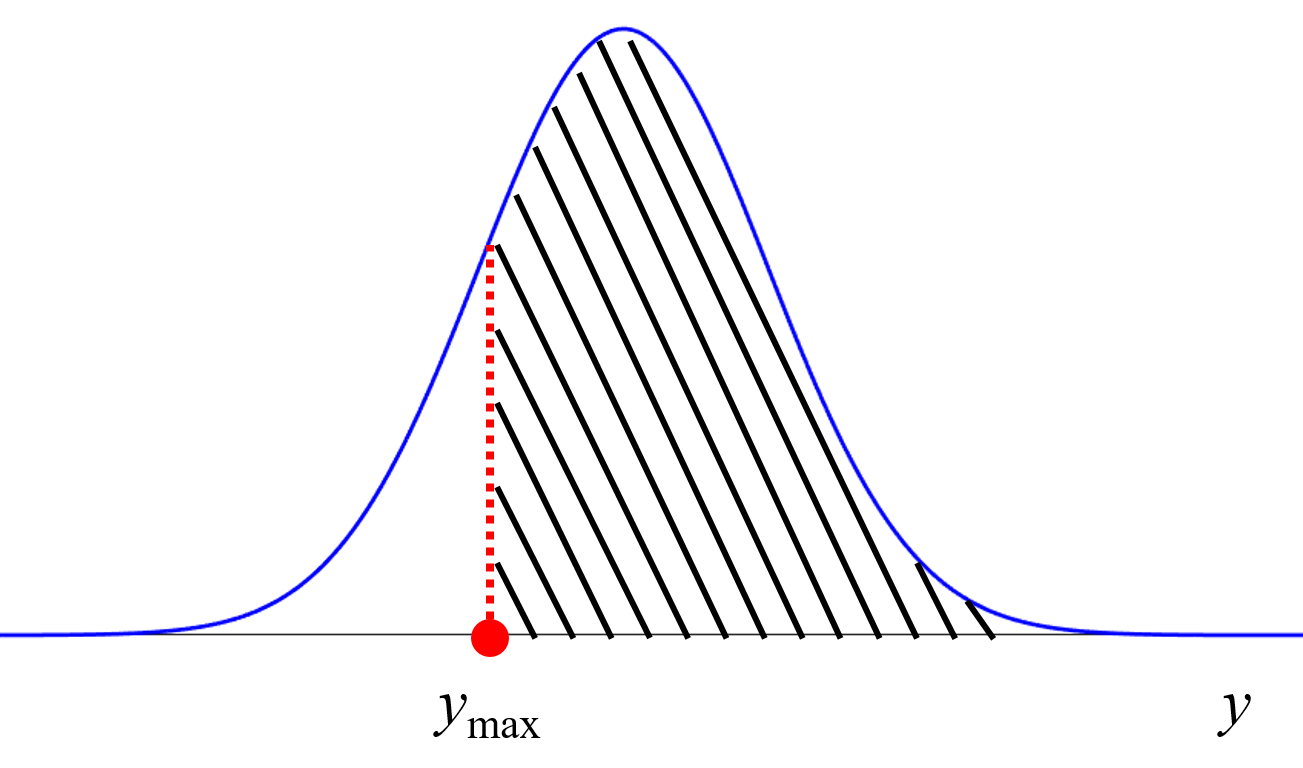
と比べて、実験回数の大幅な削減、すなわち材料開発までの効率化を達成しました。さらには、ベイズ最適化では実験を重ねるごとに徐々に Y の値が向上していく傾向が確認されましたが、GMR による適応的実験計画法では、もちろん徐々に Y の値が向上することもありますが、Y の値が急激に向上するケースが見られました。論文中の Fig. 4(f) がその例であり、興味深い結果といえます。
GMR などの直接的逆解析法でうまくいく理由については、以前にこちらで述べた通りです。

本手法は、適応的実験計画法においても有望な手法としてお勧めしておりますので、もし興味がありましたら論文をお読みいただければと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。