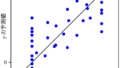
分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
構築したモデルを解釈することで、x と y の間の関係や、y が発現するメカニズムの解明に役立てようとする検討もあります。このモデルの解釈において、各サンプルにおける局所的な解釈も重要な一方で、
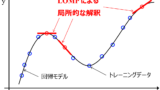
変数重要度もしくは特徴量重要度が大いに役立ちます。例えばランダムフォレストをはじめとする決定木のアンサンブル学習によって変数重要度を計算したり、
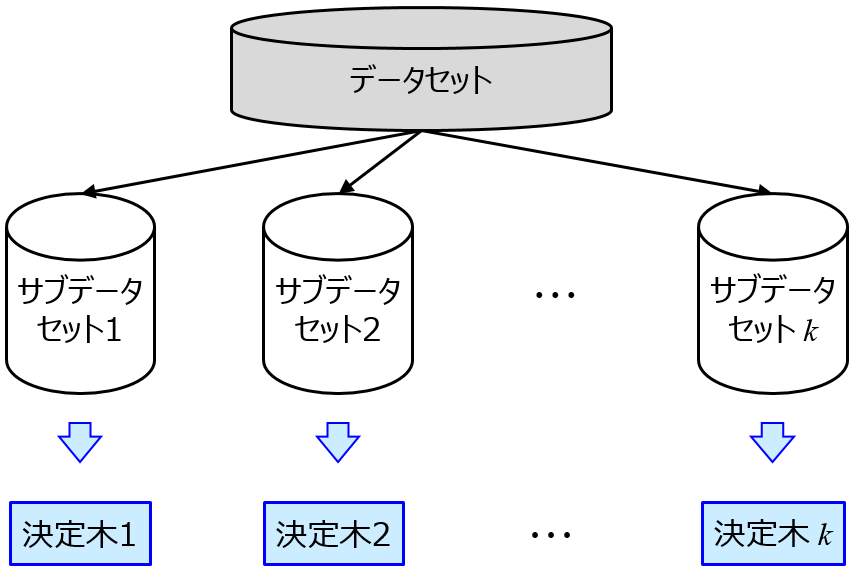
Cross-Validated Permutation Feature Importance (CVPFI) を用いることで任意の回帰分析手法において変数重要度を計算できます。
ただ、変数重要度は “そのモデルの” 変数重要度に過ぎないため、変数重要度を解釈に用いることができるかどうかは、モデルの予測精度に依存します。基本的な考え方としては、モデルの予測精度が高ければ高いほど、変数重要度の値を解釈に使用できるようになります。例えば、テストデータを予測した結果やダブルクロスバリデーションの予測結果において、r2 が 0.9 のときには、y のばらつきの 90% を説明する変数重要度という意味になりますし、r2 が 0.1 のときには y のばらつきの 10% しか説明できない変数重要度ということになります。
さらに、r2 が 0.9 といっても、実際は y の実測値 vs. 予測値プロットを確認して、y のどの値の範囲を的確に説明できるモデルなのかを確認する必要があります。例えば y の値が小さいところしか精度良く予測できないモデルのときは、変数重要度もその範囲の y のみを説明する上で重要な変数となります。
さらにいえば、r2 が負のときは、y のばらつきをまったく説明できていないため、変数重要度はあてになりません。
クラス分類における変数重要度でも同様の考え方ができます。もちろん、回帰分析における実測値 vs. 予測値プロットと同様に、クラス分類では混同行列を必ず確認して変数重要度を議論する必要があります。
さらに詳細に、変数重要度の値がいくつ以上であれば、本当に “重要” といるかどうかは、乱数を用いて検討するとよいでしょう。

変数重要度という、重要そうな値が得られたとしても、適切に使用して議論するのがよいでしょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。