金子研の論文が Digital Chemical Engineering に掲載されましたので、ご紹介します。タイトルは
Local interpretation of nonlinear regression model with k-nearest neighbors
です。
分子設計・材料設計・プロセス設計・プロセス制御・プロセス管理において、データセットを用いて目的変数 y と説明変数 x との間で構築された回帰モデル y = f(x) を活用することが一般的になっています。回帰モデルにおいて重要なことの一つは、予測精度の高いモデルを構築することです。そのため、線形の回帰分析手法だけでなく、非線形の回帰分析手法も検討します。データセットごとに、各手法で実際に回帰モデルを構築し、構築されたモデルの予測精度を評価して適切な手法を選択します。多くの場合で x と y の関係は非線形であり、本研究では非線形の回帰分析手法に着目します。
物性や活性が発現するメカニズムを解明するため、構築された回帰モデルを解釈し、y と x の間の関係を明らかにすることも重要です。例えば、cross-validated permutation feature importance (CVPFI) で線形モデルや非線形モデルにおける x の変数重要度を計算できます。
CVPFIではクロスバリデーションに基づいて、繰り返し計算の中で x の重要度を計算するため、サンプルが少ないときにはクロスバリデーションの分割数を大きくすることで、安定的に x の重要度を計算できます。相関の強い x の組があっても、適切に重要度を見積もることができます。
モデルを解釈するためデータセット全体の x の重要度を求めることも重要ですが、x に対する y の寄与を考えるときは、非線形の回帰モデルであれば、y に対する局所的な x の寄与もしくは方向性を考える必要があります。これにより、例えば y が最大値を持つサンプルに対して、さらに y の値を向上させる x の方向を議論できます。
そこで、回帰モデルのシミュレーションに基づいて x に対する y の局所的な傾きを計算する手法を提案しました。提案手法を LOcal slope of Model Prediction (LOMP) と呼びます。LOMP により、x で微分できない回帰モデルに対しても、局所的な傾きを直接的に求められます。
LOMP のイメージは以下のとおりです。
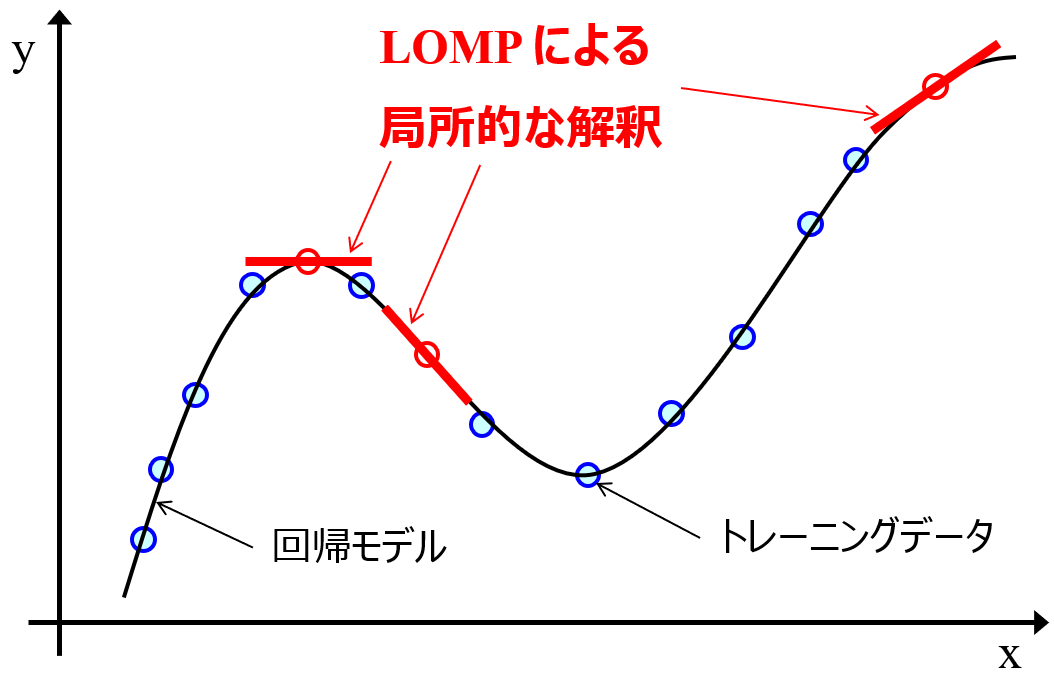
非線形の回帰モデル (上図の曲線) を構築したあとに、あるサンプルの x 周りの LOMP (上図の太い赤線の傾き) を求めたいとき、そのサンプルの x の周りに、局所的に乱数で仮想的な x のサンプルを生成します。例えば 100 サンプル生成したら、回帰モデルに入力して y を予測します。生成した x と y の予測値との間で、最小二乗法による重回帰分析で線形モデルを構築し、その回帰係数を LOMP とします。なお、たとえ元のデータセットにおいて x の間に強い相関があっても、100 サンプルはランダムで生成していますので x の間の相関は 0 であるため、多重共線性の影響はなく線形モデルの回帰係数を寄与度として信用できます。この信用できる局所的な回帰係数を、LOMP として用いて非線形の回帰モデルを局所的に解釈します。
また、モデルはデータのノイズの影響を受けるため、上の LOMP や LIME や SHAP では、ノイズの影響を受けやすいといえます。そこで本研究では、対象のサンプル周辺の k-nearest neighbors (kNN) の情報も考慮して寄与度を計算する手法を提案しました。kNN における k を 1, 2, 3, … と大きくしながら、LOMP, LIME, SHAP の kNN における値の平均値を計算します。k = 1 のときは対象のサンプルの LOMP, LIME, SHAP の値と一致し、k がトレーニングデータのサンプル数になれば、グローバルな寄与となります。LOMP を用いることで、kNN の範囲でシミュレーションして安定的に寄与を計算できるとともに、あるサンプル周りのローカルな寄与からグローバルな寄与まで連続的に求めることができます。
論文では、沸点のデータセットおよび水溶解度のデータセットを使用して、提案手法によってモデルの解釈が可能になることを検証しました。
興味のある方は、ぜひ論文をご覧いただければと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。