分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
特に低分子の有機化合物を扱う際には、分子構造から x への数値化が必要です。構造記述子や第一原理計算、グラフ畳み込みニューラルネットワークなど様々な数値化手法が存在しますが、フィンガープリントがその一つとして広く用いられています。フィンガープリントは構造検索や構造間の類似度評価に特に効果を発揮します。フィンガープリントそのものを x として用いることも有効ですが、フィンガープリントが力を発揮するのは構造間の類似度評価であることに着目した時、フィンガープリントに基づく類似度により新しい構造情報の数値化が可能になります。
例として、標準的な類似度指標の一つである tanimoto 係数を使用する場合、トレーニングデータにおける化合物の化学構造との間の tanimoto 係数を x として用いると、x の数はトレーニングデータのサンプル数と同じになります。もちろん、トレーニングデータが変わらなければ、新しい化学構造に対しても x の計算は可能です。トレーニングデータにおけるすべての化学構造との間で tanimoto 係数を計算することになります。
tanimoto 係数だけではなく、他の類似度指標も多く存在します。また、フィンガープリントの種類も一つではなく、多様なフィンガープリントが存在します。そのため、全てのフィンガープリントの種類や類似度の指標を使用すると、特徴量の数は、
(フィンガープリントの種類の数)×(類似度指標の種類の数)×(トレーニングデータのサンプル数)
になります。
これらの特徴量の全てを使用する必要はないかもしれませんが、フィンガープリントの多様性や類似度の指標の多様性によって、従来得られなかった化学構造の特徴を捉えることが可能になるかもしれません。

ちなみに、類似度を使用する方針は、化学構造の数値化に限った話ではありません。カーネル関数も類似度として考えることができ、

上で述べた方法と同様のアプローチが、実はカーネル関数を用いた手法においてはモデリングの中で当たり前のように実施されています。
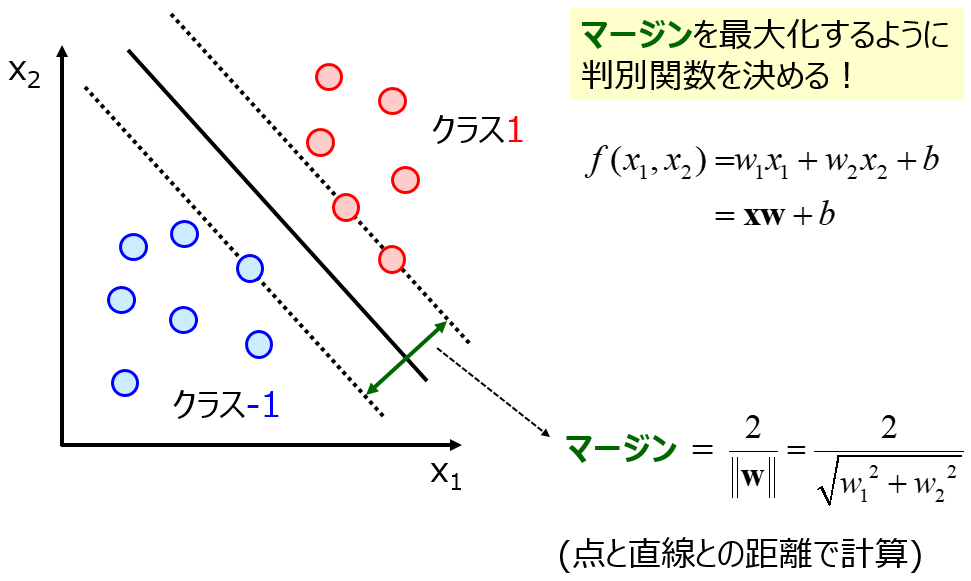


多様なフィンガープリントや多様な類似度指標に基づいて、化合物の分子構造間の類似度を有効に数値化できると良いでしょう。
以上です。
質問やコメントなどありましたら、X, facebook, メールなどでご連絡いただけるとうれしいです。


