サポートベクターマシン (Support Vector Machine, SVM) や サポートベクター回帰 (Support Vector Regression, SVR) や ガウス過程回帰 (Gaussian Process Regression, GPR) などでよく出てくるカーネル関数についてです。


カーネル関数は他にもいろいろな手法にも使えます。変数間の非線形性を考慮するための便利な関数です。カーネル関数、最高!
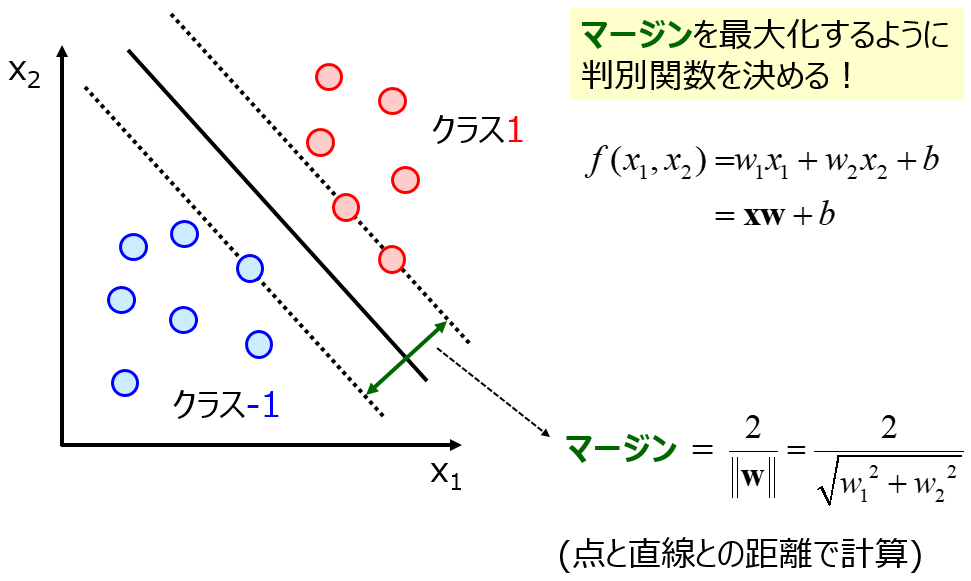
たとえば SVM では、次のような文脈でカーネル関数が出てきます。
線形の SVM モデルを定式化できた (式で表せた)!
↓
目的変数 y と説明変数 x の非線形関係を表現するために、x を非線形変換しよう!
↓
非線形変換?どんなのがよいかわからないし、とりあえず非線形関数を φ として、x → φ(x) に!
↓
SVM モデルの式で x → φ(x) としたら、2 つのサンプル間 (x(i) と x(j)) の内積 φ(x(i))φ(x(j))T しか出てこないぞ!
↓
φ が何かわからなくても、φ(x(i))φ(x(j))T さえ分かれば OK!
↓
K(x(i), x(j)) = φ(x(i))φ(x(j))T と置いて、K をカーネル関数とよぼう!
こんな感じでしょうか。詳しくはこちら ↓ をご覧ください。

カーネル関数って、φ が決めるべきときに、その内積を決めることに問題を変えただけじゃないの??そもそもカーネル関数ってどんな意味があるの??、こんなことを踏まえながら、カーネル関数について考えてみます。
まず、”x → φ(x) としたら、2 つのサンプル間 (x(i) と x(j)) の内積 φ(x(i))φ(x(j))T しか出てこない” ということは、そもそもモデルの式が、サンプル間の内積 x(i)x(j)T で表されていたということです。
サンプル間の内積の意味って何でしょうか?
その前に、回帰分析の大前提を確認します。それは、
x の値が似ていると、y の値も似ている傾向がある
です。化学構造 (x) が似ていると、その化合物のもつ物性値・活性値 (y) は似ている傾向がありますし、ある材料をつくるときの実験条件・製造条件・レシピ (x) が似ていると、その実験結果として得られる材料の特性値 (y) も似ている傾向があります。具体的には、分子量が同じように大きいと、沸点も同じように高い傾向がある、といった感じです。
回帰分析において大切なことは、いくつかサンプルがあるときに、それらの x の値がどれくらい似ているか評価することです。x におけるサンプル間の類似度を評価、と言いかえることもできます (もちろん y におけるサンプルの類似度も大事です)。
サンプル間の内積の意味に話を戻します。
2 つのサンプル間の内積は、各 x の値をサンプル同士で掛けて、すべて足し合わせたものです。各サンプルの平均値を 0 とすれば、サンプル間の内積はサンプル間の共分散と同じ意味です (正確に言えば、共分散に x の数で割ったものと一致します)。
共分散は、相関係数に互いの標準偏差を掛けたものであり、値が正や負に大きいほど相関が高く (似ており)、0 に近いほど相関が低い (似ていない) といえます。つまり、サンプル間の類似度のようなものです。
サンプル間の内積で、回帰分析で大切な、サンプル間の類似度を評価していたわけです。
ただし、共分散で評価できるのは、2 つのサンプルの傾きが (他の2つのサンプルと比べて) 似ているかどうかだけです。直線的な類似度です。たとえば、ある 2 つのサンプルが近くにあって、また別の 2 つのサンプルが近くにあっても、それぞれにおけるサンプルの傾きが異なると、サンプル間の類似度は異なってしまいます。
サンプル間の類似度を、サンプル間の内積だけでなく、いろいろと評価しようというのが、カーネル関数です。たとえば、よく使われるガウシアンカーネル Radius Basis Function (RBF) を見てみましょう。
K(x(i), x(j)) = exp(−γ||x(i)−x(j)||2)
サンプル間のユークリッド距離 d = ||x(i)−x(j)|| があります。2 つのサンプル間の距離が近いほど、それらのサンプルは似ているといえますので、サンプル間の類似度となりそうです。ただ距離は、値が小さいほど類似度が高くなり、類似度と逆の大小関係になります。そこで、exp(−γd2) と変換して、値が大きいほど類似度が高い、としたわけです (厳密にいえば他にも理由はあります)。0 から 1 までの値をとり、1 に近いほど 2 つのサンプル間は似ているといえます。
このように、カーネル関数は、サンプル間の類似度を評価するものです。関数を変えることで、いろいろな類似度を評価できます。類似度でしたら、tanimoto 係数などいろいろな指標がありますし、非線形関数 φ よりは考えやすいだろう、というわけです。
扱うデータセットにおいて、サンプル間の適切な類似度がある場合は、それをカーネル関数にするとよいと思います。ただし、他にもカーネル関数のルールがありますので、たとえばこちらの本などで調べてからにしましょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


