サンプル数が小さいデータセットには、データ解析で回帰分析やクラス分類をするとき、とてつもなく大きな問題があります。回帰分析やクラス分類における問題というと、精度の高いモデルが構築できないことを想像するかもしれません。
逆です。
精度の高いモデルができてしまうことが問題
なのです。
説明します。
話を単純にするため、小さなサンプル数のデータセットを用いて、最小二乗法による線形重回帰分析 (Ordinary Least Squares, OLS) を行うこと考えます。
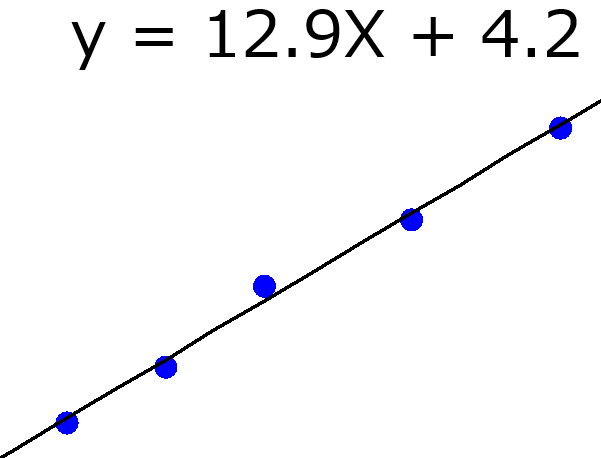
OLS では、目的変数におけるサンプルの誤差の二乗和を小さくするように、各説明変数の係数 (回帰係数) を決めます。サンプル数が小さく、説明変数の数が大きいとき、小さくしなければならない誤差の数は小さい一方、自由に値を変化できる回帰係数の数は大きいです。つまり、誤差を小さくしやすい状況といえます。
なので、たとえば乱数のような、目的変数とまったく関係のない変数でも、説明変数に (たくさん) あったとき、偶然に目的変数とあってしまう (誤差が小さくなってしまう) 可能性が高くなります。説明変数の組み合わせで、目的変数の誤差を小さくするよう回帰係数を決めますので、誤差の二乗和が偶然に小さくなることも多いわけです。
他の回帰分析・クラス分類手法でも同じような状況です。OLS では自由に変化できるパラメータである回帰係数の数が、説明変数の数と同じでしたが、特にニューラルネットワークなどの非線形モデルでは、パラメータの数が OLS と比べて多く、さらに誤差を小さくしやすい状況です。
結果的に、説明変数と目的変数との間の、本質的な関係にかかわらず、精度の高いモデルが構築されてしまうわけです。
精度の高いモデルができた!、と喜ぶのはよいですが、実際には意味のないモデルである可能性も高いのです。このような誤解が大きな問題なのです。モデルの精度は高いと誤解して、新たなデータの予測を行っても、予測は当たりません。これだけでも問題ですし、統計モデルや機械学習に対する信頼が失われてしまうことも、また問題です。
クロスバリデーションで検証しているから大丈夫では??
構築したモデルの予測精度は、クロスバリデーションで検証済み!、と考える方もいらっしゃるかもしれません。しかし、クロスバリデーションも万能ではありません。サンプル数が小さく説明変数の数が大きい状況では、クロスバリデーションの結果も偶然によくなってしまうことがあります。さらに、クロスバリデーションで評価した結果を最適化に使用しているときの問題について、こちらをご覧ください。

じゃあどうすればいいの??サンプル数がいくつ以上なら大丈夫なの?
サンプル数が小さいときの問題は根が深いです。もちろん、サンプル数が小さいデータセットの中にも、目的変数と説明変数との間に本質的な関係があるかもしれません、しかし、サンプル数が少ないと、本質的な関係の有無にかかわらず、精度の高いモデルが構築されてしまう可能性があるのです。なので、本質的な関係があるかないかを調べることは難しいです。
本質的な関係を抽出するために必要なサンプル数は、説明変数の数や説明変数と目的変数との関係にも関わるため、つまりデータベースによって変わるため、いくつ以上なら OK !、とはいえません。
できることは、そのデータセットを用いたときに、偶然による精度の高いモデルの構築されやすさがどれくらいか、を検証することです。これには yランダマイゼーション (y-randomization or y-scrambling) を用います。

yランダマイゼーションで、chance correlation (偶然の相関) の危険度を評価します。yランダマイゼーションしたときにも、精度の高いモデルが構築されてしまったら?残念ながら、目的変数の値をシャッフルする前の正しいデータセットでも、精度の高いモデルが構築されたのは偶然の可能性が高いです。
yランダマイゼーションでも精度の高いモデルが構築されてしまったら、あきらめるしかないの??
yランダマイゼーションでも結果がよくなってしまった場合、つまり今のデータセットでは偶然に精度の高いモデルが構築される可能性が高い場合、の対処法はあります。それは、データ解析をすることなく、主観的に変数選択することです。目的変数を説明するために大事で、しかもなるべく小さい数の説明変数を手動で選んでください。
yランダマイゼーションでも結果がよくなりやすい (=偶然に精度が高くなる危険が高い) のは、サンプル数が小さく、説明変数の数が大きい場合です。サンプル数を増やすことは難しいので、説明変数の数を減らすわけです。説明変数を選択して、数を減らした後に、再びモデル構築したり、yランダマイゼーション後にモデル構築したりしましょう。モデル構築したときの精度は高いままで、yランダマイゼーション後にモデル構築したときの精度が低くなっているとうれしいわけです。
大事なことは、データ解析や機械学習の手法では説明変数を選択してはいけない、ということです。基本的に手法を使った説明変数の選択では、モデルの精度が高くなるように、変数選択します。結局、目的変数との間に偶然に相関のある説明変数の組み合わせが選ばれてしまうわけです。言い方をかえると、yランダマイゼーション後に変数選択しても、モデルの精度が高くなるような変数が選ばれてしまいます。
小さなデータセットは、大きな問題を抱えていることを理解して、適切に対処しましょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。