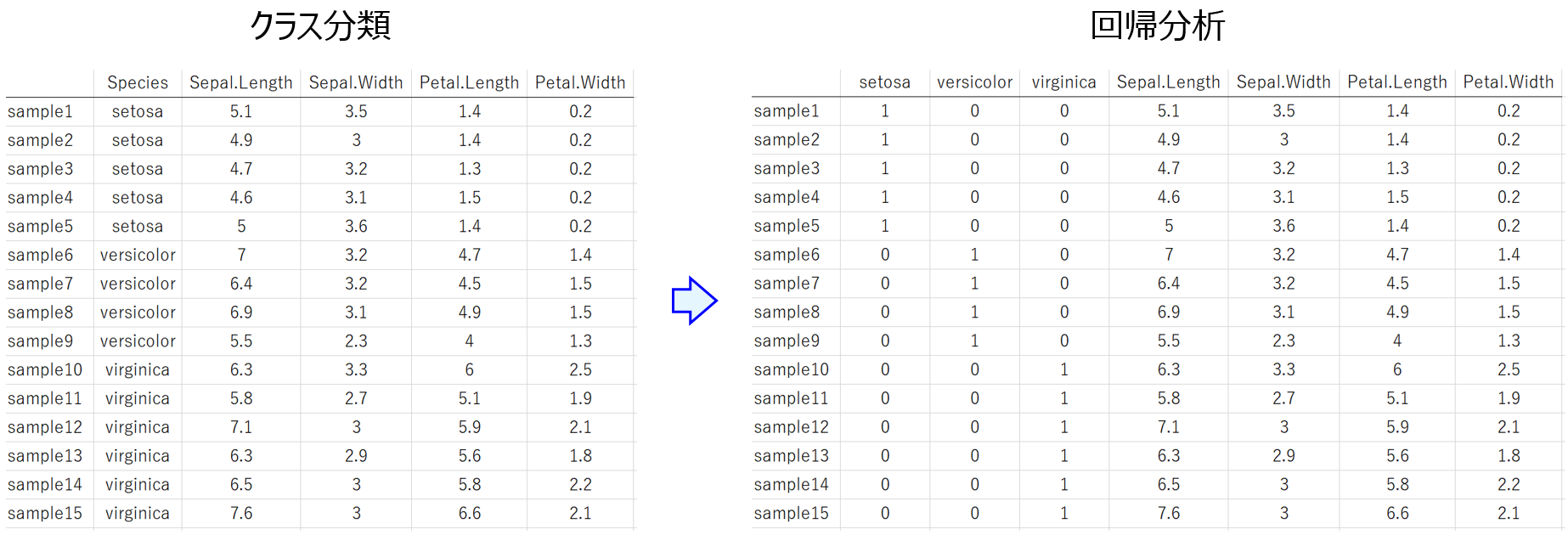
教師あり学習には、大きく分けてクラス分類と回帰分析があります。目的変数が連続値であれば回帰分析、サンプルごとのクラスの情報であればクラス分類です。変数のレベル的には、回帰分析の目的変数が間隔尺度もしくは比例尺度、クラス分類の目的変数が名義尺度もしくは順序尺度といえます。

ちなみに、クラス分類でも回帰分析でも、説明変数 (記述子・特徴量) は間隔尺度もしくは比例尺度でなければいけません。
今回は、クラス分類の目的変数を、回帰分析の目的変数に変換する方法を紹介します。クラスのデータを、連続値に変えるわけです。名義尺度もしくは順序尺度の変数を、間隔尺度に変換できるので、サンプルごとのクラスの情報を説明変数 (記述子・特徴量) として用いたい場合にも使える方法です。
iris (あやめ) のデータセットで説明します。ここでは見やすくするため、あやめのサンプルを減らしています。
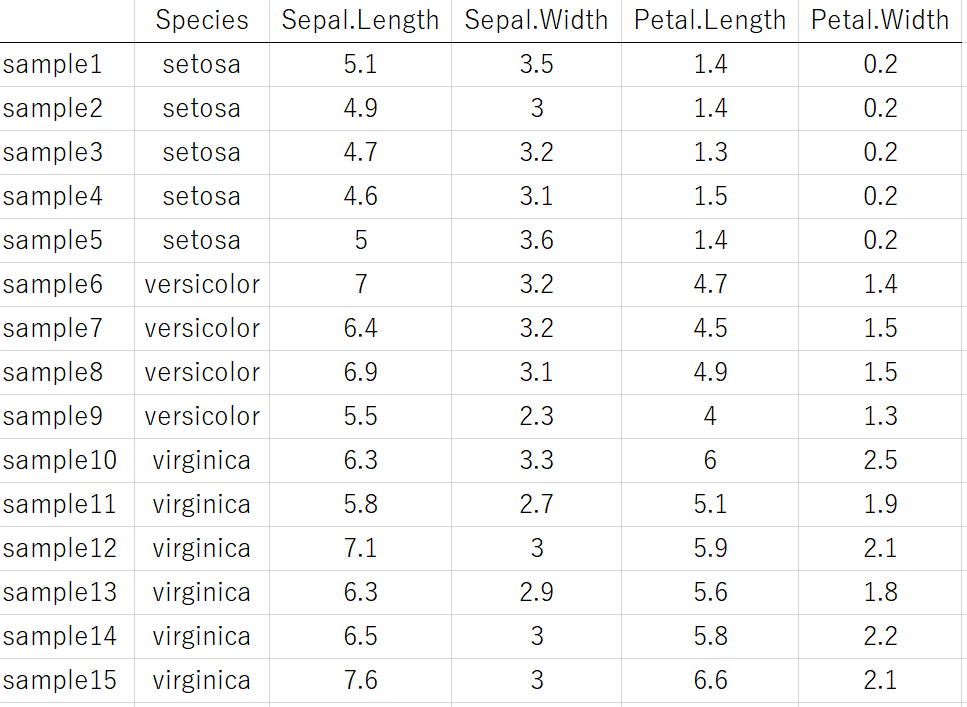
一番左に、あやめの種類 (setosa, versicolor, virginica) というクラスの情報があります。クラス分類では、これが目的変数になるわけです。これを回帰分析のためのデータにするには、次のように変換します。
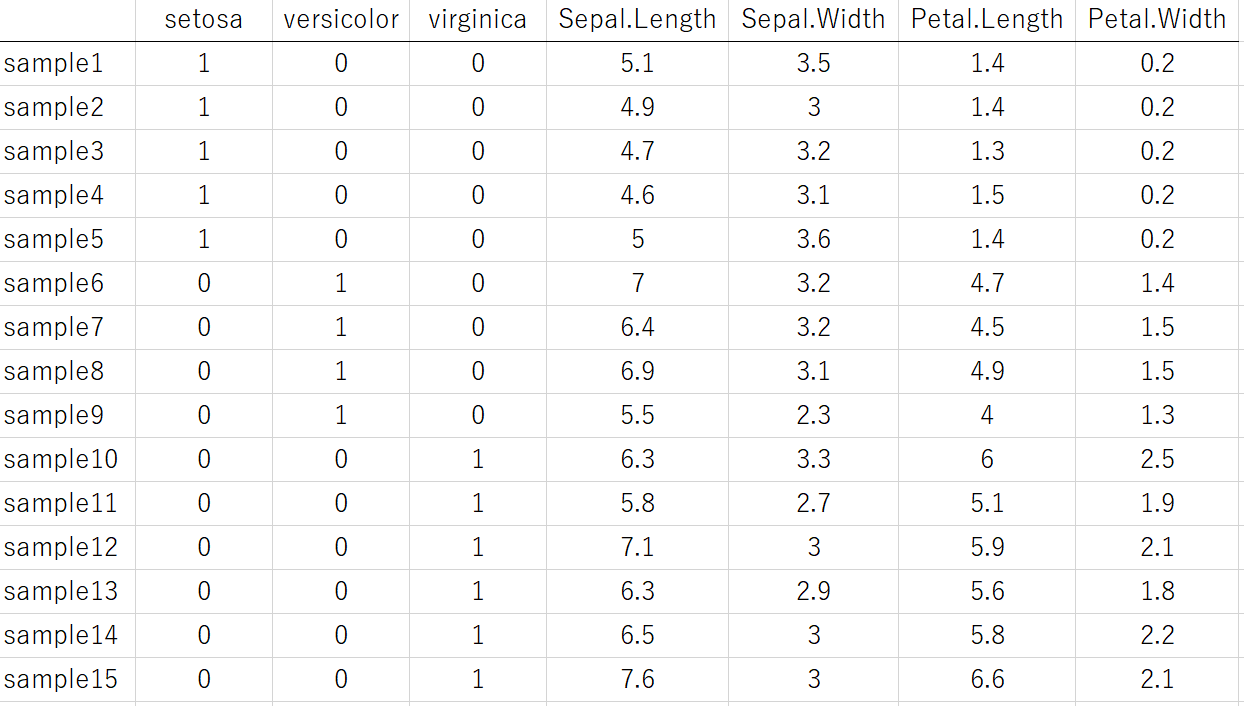
setosa, versicolor, virginica それぞれについて、1 もしくは 0 が入る変数になっていることが分かります。たとえばsample1はsetosaなので、setosaの変数だけ1で、他の versicolor と virginica の変数は 0 になります。
このように、クラスごとに そのクラスのサンプルだけ 1 になるような 0, 1 の変数にすることで、クラス分類の問題を、回帰分析の問題に変換することができます。クラスの数が、回帰分析における目的変数の数になるわけです。
ちなみにこの変換は、one-hot 表現とか、one-hot ベクトルとか呼ばれたりもします。
複数の目的変数がある回帰分析になります。目的変数ごとに回帰モデルを構築してもよいですし、複数の目的変数を同時に扱える手法のときは、1つの回帰モデルを構築してもよいです。
注意点として、下のようにしてはいけません。
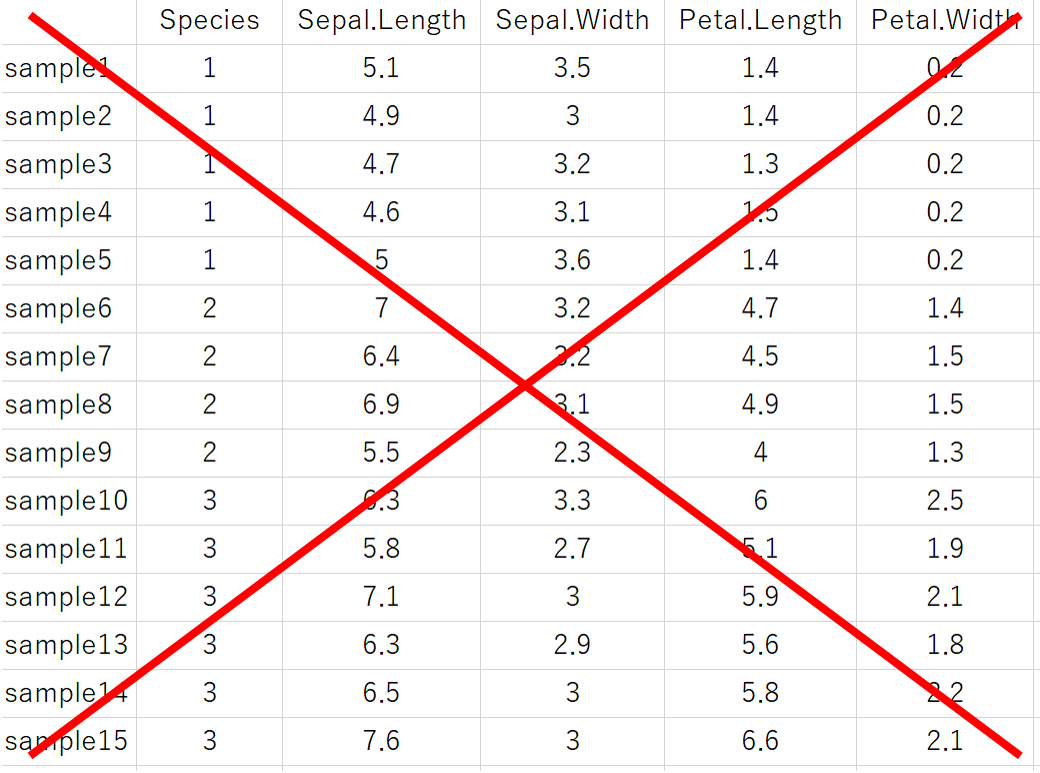
一見、Species は数字なので、これを目的変数にして回帰分析できそうですが、これは名義尺度なので回帰分析の目的変数として使うことはできません。virginica と setosa の差 (3–1=2) が、versicolor と setosa の差 (2-1=1) の2倍あるわけではありませんよね。
今回説明した方法は、名義尺度もしくは順序尺度を間隔尺度に変換する方法です。なので、たとえば説明変数にクラスの変数があるとき、そのままでは説明変数として使えませんが、今回の方法でクラスごとに 0, 1 の変数に変換すれば、説明変数として用いることができます。
ぜひご活用ください。
なお、この変換は one hot encoding とか one-hot 表現とか、one-hot ベクトルとか呼ばれたりもしまして、scikit-learn にも実装されています。

以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。