回帰モデルやクラス分類モデルを構築するとき、データセットの前処理や特徴量の低次元化を目的として、主成分分析 (Principal Component Analysis, PCA) を行うことがあります。

可視化・低次元化の手法としては最も基本的な線形手法であり、最も単純な手法といってよいと思います。他の様々な高度な手法や非線形手法がある中で、
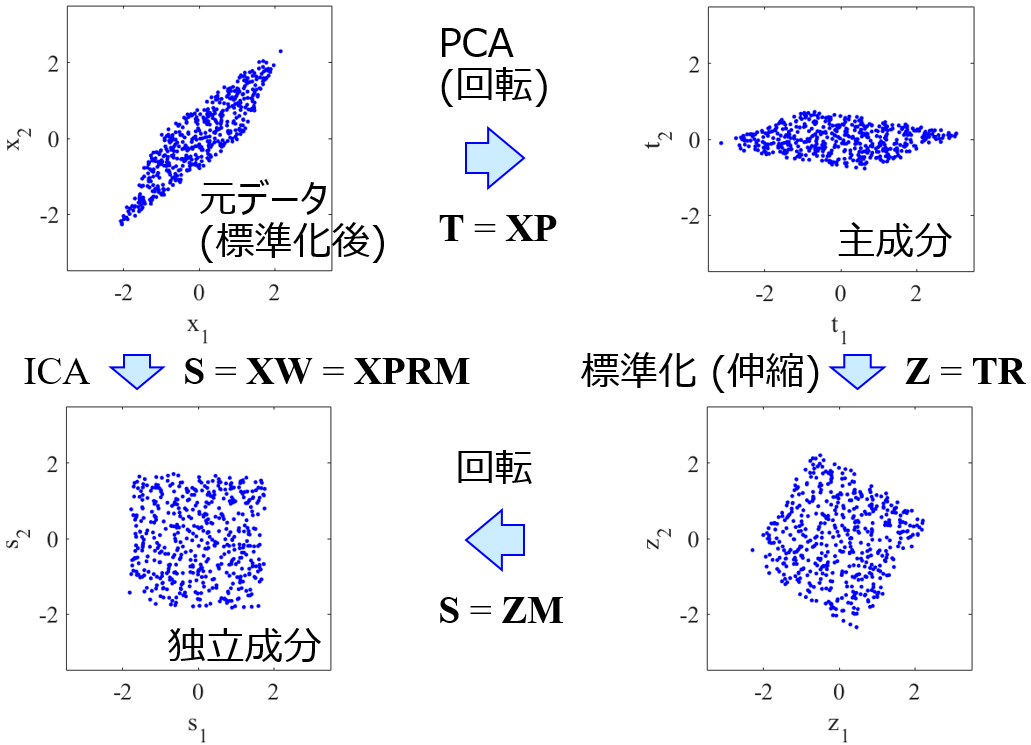
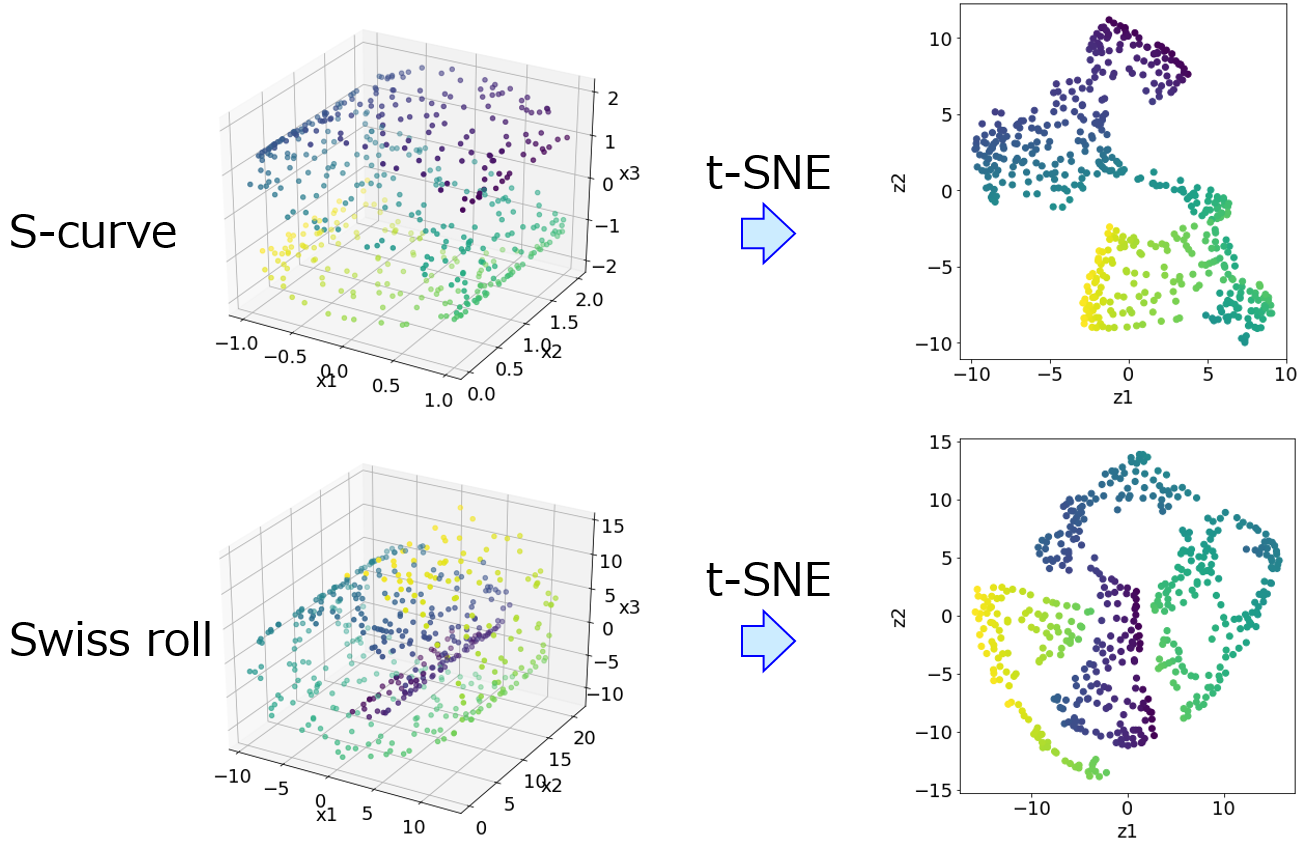

PCA に物足りなさを感じる人もいらっしゃるかもしれません。特徴量間の非線形性を考慮できる GTM や DAE など、手の込んだ手法を使いたくなる人もいらっしゃるでしょう。もちろん、これらの手法によりモデルの予測精度が向上することはありますが、いつもそうなるとは限りません。もしろ、データセットの準備に工夫を入れて、データセットが複雑なものになればなるほど、今のデータセットに適した方法を工夫して、シンプルな PCA を使用する方が的確に特徴量を抽出できたりもします。
例えば、高分子材料データにおける複数の原料や、有機合成反応データにおける触媒や基質など、複数の分子の組み合わせが一つのサンプルになっているときを考えます。サンプルの特徴量を考えるとき、一般的には、まず分子ごとに分子記述子を計算し、組成比をからめて特徴量にしたり、分子記述子を横につなげて特徴量にしたりして、場合によっては重合条件や合成条件など別のパラメータも横につなげて、説明変数 x を準備してから、PCA を実行します。ただ、分子の立場になって考えると、複数のサンプルで同じ分子が使われていると情報を圧縮するという観点では効率的でなかったり、重合条件や合成条件など分子記述子とは関係のない基本的には相関関係のない特徴量があったりと、PCA が本領発揮できる状況ではありません。
この場合は、使用する (重複なしの) 分子だけ集めて別途データセットを作り、これに対して PCA を行い、分子記述子を潜在変数に変換してから、その潜在変数を分子記述子の代わりに使用する方が効率的です。
プロセスデータにおいても、すべてのプロセス変数を横につなげて x にしたり、プロセス変数から特徴量を抽出してからまとめて x にしたりしてから、PCA を行うのが一般的です。ただ、複数の単位操作が順番に行われるときなど、プロセスが複雑になればなるほど、単位操作のプロセス変数ごと、単位操作ごとに抽出した特徴量ごとに PCA をしてから、それぞれ抽出された潜在変数をまとめて x とするほうが効果的に情報圧縮できる場合があります。
以上のような工夫をせずに、とりあえず非線形手法を使ってなんとかすることで、同じようなことができる可能性もありますが、データセットの背景・バックグラウンド、扱うデータの素性や意味合いを考えて、扱いを工夫してから、線形手法の PCA を使うほうが、頑健な (ロバストな) 情報圧縮ができたり、意味のある潜在変数の抽出ができたりします。また PCA は寄与率や累積寄与率により抽出した情報量を検討できたり、ローディングで主成分の向きを確認できたり有用なこともあります。ぜひデータセットをよく観察し、よく考え、適切な前処理や低次元化を行うとよいでしょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


