[Pythonコードあり] 教師あり混合ガウスモデル(Supervised Gaussian Mixture Models)で回帰分析も逆解析も自由自在に♪～Gaussian Mixture Regression(GMR)～

2018.09.03

混合ガウスモデル (Gaussian Mixture Models, GMM) を教師あり学習に対応させた Gaussian Mixture Regression (GMR) について、pdfとパワーポイントの資料を作成しました。GMM についてはこちらをご覧ください。

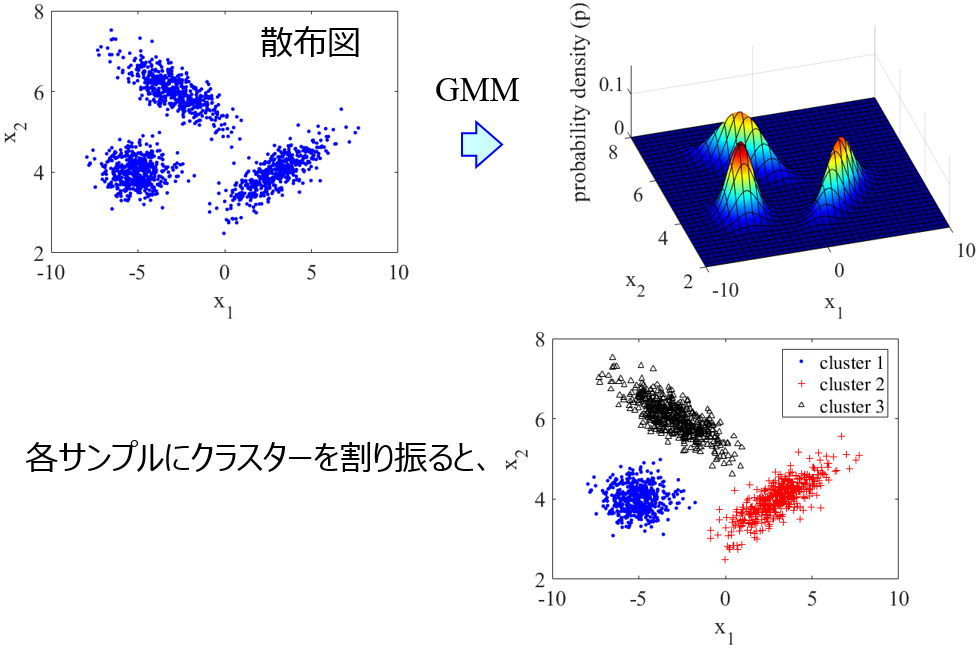
混合ガウスモデル (Gaussian Mixture Model, GMM)～クラスタリングするだけでなく、データセットの確率密度分布を得るにも重宝します～
クラスタリングについては、階層的クラスタリングと k-means クラスタリングをやりました。今回は、混合ガウスモデル (Gaussian Mixture Model, GMM) というクラスタリングの手法です。GMM を使うことで、データ...
datachemeng.com
2018.03.25

 

GMR により、回帰分析だけでなくモデルの逆解析がシンプルかつ簡単にできます。Inverse QSAR や inverse QSPR に応用できるオススメの手法です。データセットが与えられたときに、GMR で何ができるか、GMR の特徴、どのように計算するかが説明されています。pdfもスライドも自由にご利用ください。

pdfファイルはこちらから、パワーポイント(pptx)ファイルはこちらからダウンロードできます。

興味のある方はぜひ参考にしていただき、どこかで使いたい方は遠慮なくご利用ください。

 

 

また GMR や GMR の正規分布の数や分散共分散行列をベイズ情報量規準 (Bayesian Information Criterion, BIC) で最適化するコードも公開します。デモンストレーション付きです。こちらのGithubからご利用ください。

GitHub - hkaneko1985/sgmm: Supervised Gaussian Mixture Models
Supervised Gaussian Mixture Models. Contribute to hkaneko1985/sgmm development by creating an account on GitHub.
github.com

 

[New] こちらの DCEKit で、便利に GMR をご利用いただけます。

DCEKit (Data Chemical Engineering toolKit) を PyPI にリリース！
これまで化学データ・化学工学データのデータ解析に役立つツールや金子研で開発された手法に関する Python コードを Github にて公開してきました。このたびは、これらのツール・手法 (の一部) に加えて、新たな機能を追加して、DCEK...
datachemeng.com
2019.08.18

 

GMR とは？

  • 説明変数 X と目的変数 Y の関係を、複数の正規分布の重ね合わせで表現する手法
  • Y の変数が複数の場合でも、それらの関係を考慮しながら、他の手法と組み合わせることもなく、回帰分析および逆解析をすることが可能
  • 逆解析においても、モデルの適用範囲を考慮した解が得られる
  • X と Y を合わせて混合ガウスモデルを構築
    • 混合ガウスモデル (Gaussian Mixture Models, GMM) についてはこちら
混合ガウスモデル (Gaussian Mixture Model, GMM)～クラスタリングするだけでなく、データセットの確率密度分布を得るにも重宝します～
クラスタリングについては、階層的クラスタリングと k-means クラスタリングをやりました。今回は、混合ガウスモデル (Gaussian Mixture Model, GMM) というクラスタリングの手法です。GMM を使うことで、データ...
datachemeng.com
2018.03.25
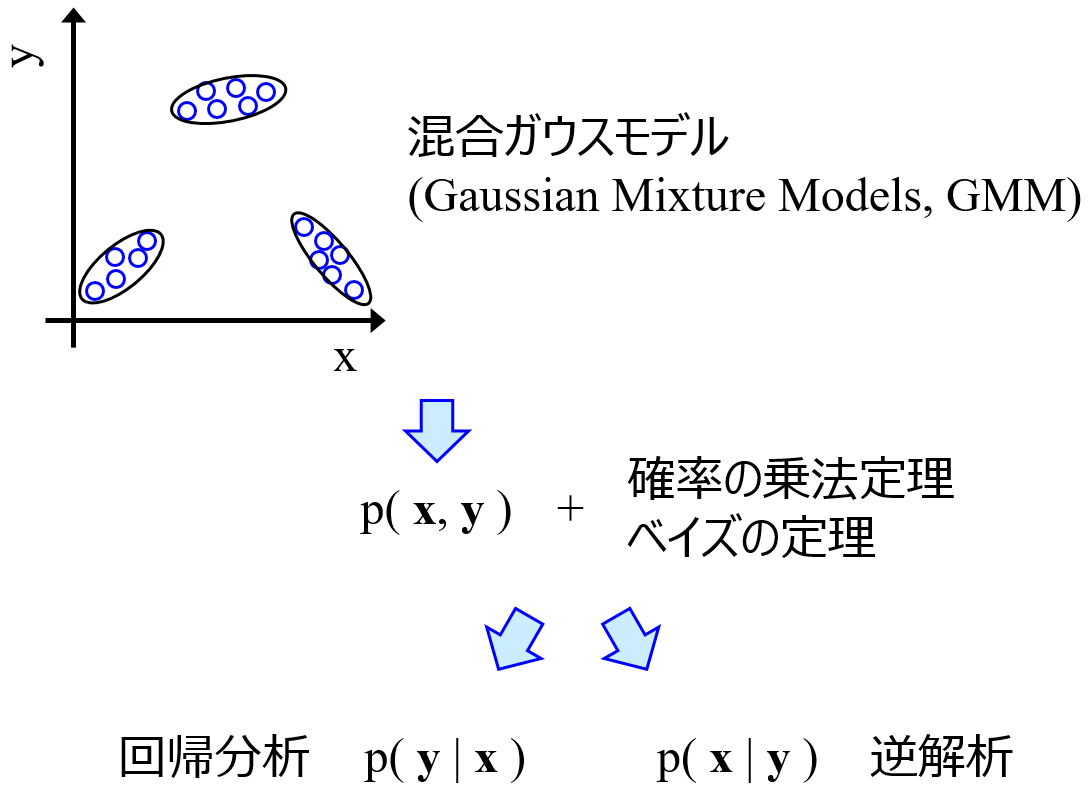
  • GMM は X と Y の同時確率密度分布 p(X, Y) に対応
  • 確率の乗法定理とベイズの定理から、p(Y|X) を求めれば回帰分析、p(X|Y) を求めれば逆解析
  • 一般的な GMR ではモデルパラメータを Expectation–Maximization (EM) アルゴリズムで計算
  • モデルパラメータを変分ベイズ法で求める GMR は Variational Bayesian GMR (VBGMR)

 

スライドのタイトル

  • GMR とは？
  • GMR の概要
  • 混合正規分布 (混合ガウス分布)
  • [参考] モデルパラメータの決め方
  • X と Y を明示的に分けて書く
  • X から Y の推定 (回帰分析)
  • Y の推定値の混合正規分布とその重み
  • Y の推定値の(多変量)正規分布の平均
  • Y の推定値の正規分布の重み
  • 最終的な Y の推定値をどうするか？
  • Y から X の推定 (逆解析)
  • 正規分布の数をどう決めるか？
  • 正規分布の数をどう決めるか？ 補足
  • その他
  • どうやって実際に GMR を実行するか？
  • 参考文献

 

参考文献

  • T. Miyao, H. Kaneko, K. Funatsu, J. Chem. Inf. Model., 56, 286-299, 2016
  • C.M. Bishop, パターン認識と機械学習 上下, 丸善出版, 2006

 

以上です。

質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。

タイトルとURLをコピーしました