応化先生と生田さんが、階層的クラスタリング(クラスター分析)について話しています。
応化:今日は階層的クラスタリングの話をします。
生田:よろしくお願いします。クラスタリングって、クラス分類と名前の似ているアレですよね。
応化:そうですね。もし違いがあやふやな場合は、こちらで復習しましょう。

生田:つまり、サンプルとサンプルとがどれくらい似ているか、が分かったときに、サンプルをいくつかの塊 (クラスター) に分けるってことですよね。
応化:その通り。今回は、その中で階層的クラスタリングをやります。
生田:階層的って何ですか?
応化:その説明をするために、実際に階層的クラスタリングを実施した結果を最初に見てみましょう。使ったデータは、こちらから作成した、北海道・東北地方・関東地方の面積と人口のデータです。
| 面積 [km2] | 人口 [人] | |
| 北海道 | 83424 | 5422560 |
| 青森県 | 9646 | 1311856 |
| 岩手県 | 15275 | 1283100 |
| 宮城県 | 7282 | 2330240 |
| 秋田県 | 11638 | 1024144 |
| 山形県 | 9323 | 1128083 |
| 福島県 | 13784 | 1915976 |
| 茨城県 | 6097 | 2914366 |
| 栃木県 | 6408 | 1973664 |
| 群馬県 | 6362 | 1972220 |
| 埼玉県 | 3798 | 7265574 |
| 千葉県 | 5158 | 6220548 |
| 東京都 | 2191 | 13516279 |
| 神奈川県 | 2416 | 9127648 |
生田:やっぱり北海道は面積が大きくて、東京都は人口が多いですね。西の方の都道府県のデータはないんですか?
応化:47都道府県をクラスタリングすると、数が多くて見えにくかったので、北海道・東北地方・関東地方のみにしました。これら14の都道府県を階層的クラスタリングすると、下のようになります。
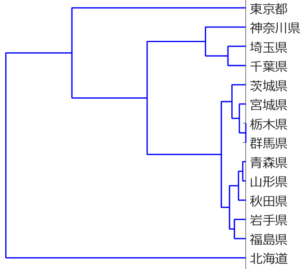
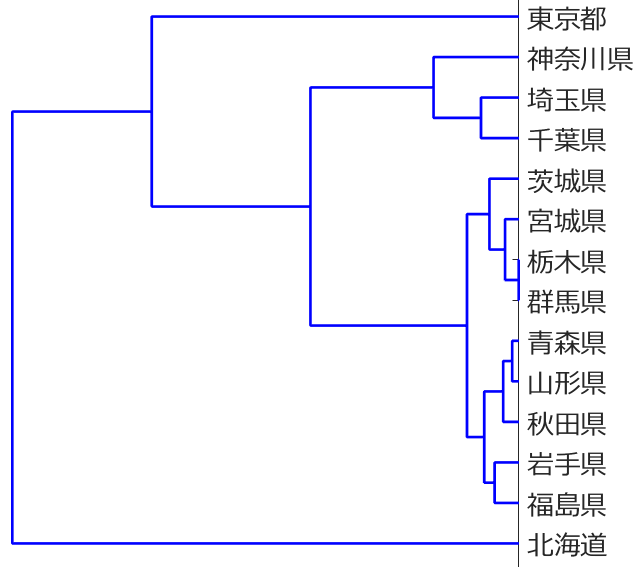
生田:なんかトーナメント表みたいですね。
応化:似ていますね。ちなみにデンドログラム (dendrogram) っていいます。
生田:対戦してるんですか?
応化:いえ、その逆です。トーナメント表でいう対戦は、その足にある2つが同じ仲間 (塊、クラスター) として結合していることを表します。よく見ると、足の長さが異なりますね。足の長さが短いものほど、先にクラスターになるってことです。
生田:栃木県と群馬県の足が一番短いですね。この2つが一番似ているってことですか?
応化:そうです。やっぱり栃木県と群馬県は似ていたんですね。逆に、東京や北海道は、足が長いので他の都道府県と似ていないということです。このように、クラスターになる順番がわかり、デンドログラムの形で見える化できるので、”階層的” クラスタリングといいます。
生田:へー。デンドログラムを見ると、上の方に人口が多いのがあって、下の方に東北地方がありますね。
応化:そうですね。関東の中でも東京に次いで人口の多い、神奈川・埼玉・千葉がかたまっているのは納得ですね。あと、東北地方の県は、関東地方と比べて面積が大きいので、かたまっているのでしょう。
生田:あ、栃木・群馬・茨城のかたまりに宮城がある!
応化:宮城は東北地方の中でも面積が小さく、北関東の3県と似ているのでしょう。このように、実際にクラスタリングすると、意外!って思える結果も出てくるので面白いですよ。もちろん、今回は面積と人口のデータだけでクラスタリングしましたが、例えば平均年齢や平均年収など、他にも変数 (パラメータ) を追加するとまた違った結果になります。
生田:わかりました!では、どのようにすればこのデンドログラムを書けるようになるのか、教えてください!
距離の近いものを結合して一つのクラスターにする、それだけ!
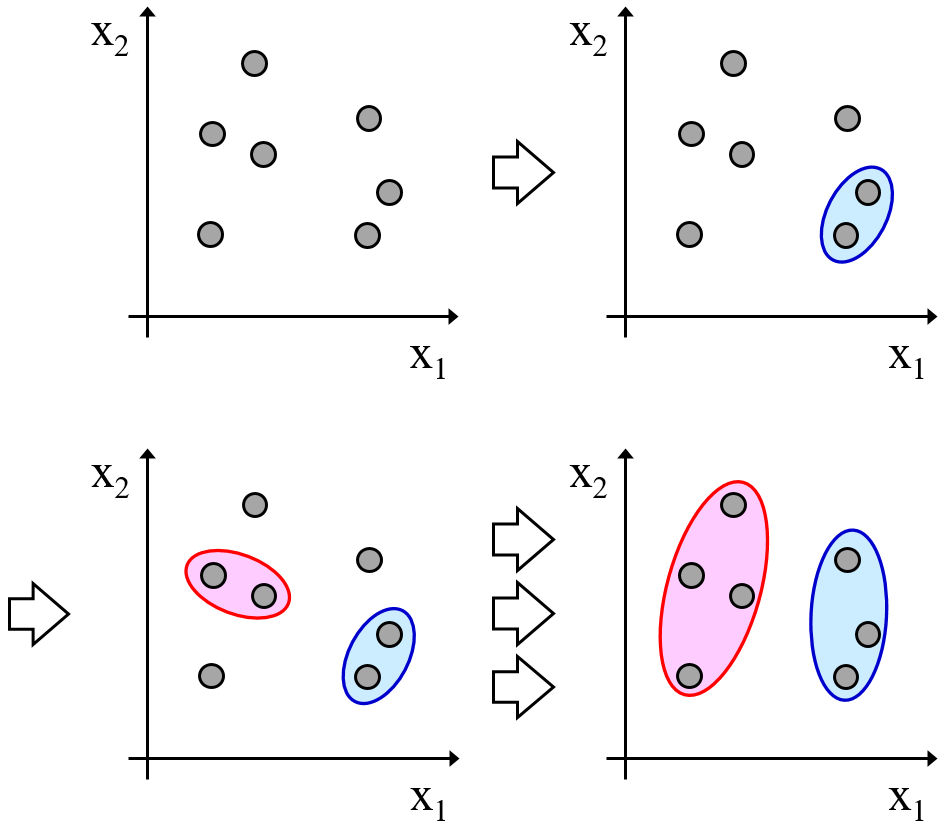
応化:では説明しますね。まず最初に、それぞれのサンプルが一つずつのクラスターであるとします。
生田:東京都も、栃木県も、群馬県も、それぞれが一つのクラスター?
応化:はい。それがスタートです。
生田:14クラスターからスタート、と。
応化:次に、すべてのクラスター間の距離を計算します。単純な距離は、たとえば2点(1,5) と (2,3) との間の距離が、
![]()
で計算されるユークリッド距離です。
生田:14の都道府県の間すべてで距離を計算するんですね。
応化:その通り。そして、距離が一番近い2つを一つのクラスターとして結合します。
生田:あ、栃木県と群馬県が一番近かったのか!
応化:そうです。今のクラスターの数は?
生田:えっと、最初14だったのが、2つが結合することで1つ減ったから、13!
応化:その通り。次は、13のクラスター間の距離の中で、最も近い2つのクラスターを結合します。
生田:またクラスターの数が1つ減った!
応化:これを繰り返すことで、どんどんクラスターの数を減らしていくのです。
生田:ちょっと待ってください。最初に栃木県と群馬県が1つのクラスターになりました。次に青森県と山形県が1つのクラスターになりました。では、(栃木県・群馬県クラスター) と (青森県・山形県クラスター) の距離はどうやって計算するんですか?
応化:いいところに気付きましたね。このようなクラスター間の距離をどうするか、で方法が分かれます。ここでは4つ紹介しましょう。
最近隣法:クラスター同士で、最も近いサンプル同士の距離
最遠隣法:クラスター同士で、最も遠いサンプル同士の距離
重心法:クラスター内のサンプルの重心(平均) の間の距離
平均距離法:クラスター同士で、すべてのサンプル間の距離の平均
生田:4つもあるんですね。
応化:ちなみに、上のデンドログラムは平均距離法で計算しました。
生田:平均距離法が一番よいのですか?
応化:そういうわけではありません。どれが一番というのはないので、いくつか計算してみて、試行錯誤するのが一般的です。
生田:そうですか、大変そうですね。
応化:ただ、まだ説明していないウォード法というのがありまして、少し複雑なので最後に説明しますが、これが一番使われていますので、迷ったらウォード法がよいでしょう。
生田:わかりました、楽しみにしています!
応化:以上をまとめますと、まずはそれぞれのサンプルを一つのクラスターとして、近いクラスター同士を次々に結合して新たなクラスターとすることで、クラスターの数を減らしていきます。クラスター間の距離として、最近隣法・最遠隣法・重心法・平均距離法があります。よろしいですか?
生田:OKです!
応化:ちなみに、上のデンドログラムの足の長さは、クラスター間の距離に対応しています。距離が大きいほど、あとで結合するクラスターってことです。
生田:なるほど。
応化:そして、デンドログラムの足をどこで切るか、によってクラスターの数が決まります。
生田:足を切る?
応化:下の図のようなイメージです。
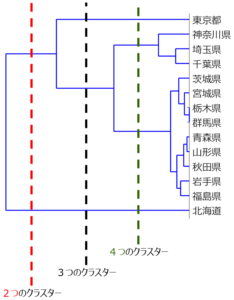
生田:赤で切ったら2つのクラスター、黒で切ったら3つのクラスター、緑で切ったら4つのクラスターってことですか?
応化:その通り!
距離といってもいろいろある
応化:クラスタリングの基本的なことは、以上です。
生田:ありがとうございました。
応化:一つ、先ほどは距離としてユークリッド距離を用いていましたが、他にもいろいろな距離があります。
生田:たとえば?
応化:マハラノビス距離、マンハッタン距離、チェビシェフ距離などです。
生田:いろいろありますね。
応化:興味があったら Google などで調べてみるとよいでしょう。たとえば、変数(パラメータ)の間に相関があるときは、マハラノビス距離が有効です。
生田:わかりました。
応化:さらに言うと、距離でなくても類似度を表すものでも対応可能です。
生田:どうしてですか?
応化:距離っていいかえると、非類似度ですよね。距離が大きいほど似ていない、つまり、類似度が小さい。
生田:確かに。
応化:なので、tanimono係数、コサイン類似度のような類似度を、逆数にしたり1-類似度にしたりして非類似度にすれば、距離として使えるのです。相関係数は負の値を取るので、1-相関係数が妥当ですね。
生田:どういうときに類似度を使いますか?
応化:たとえば、変数間の相関に着目したいときは、相関係数がよいでしょう。また、化学構造のfingerprintのような、0・1で表される変数のときは、tanimoto係数がよいです。
生田:わかりました!
ウォード法
応化:最後に、ウォード法です。
生田:複雑なやつですよね。大丈夫かなぁ。
応化:ここまでついてこれたなら大丈夫ですよ。
生田:がんばります!
応化:ウォード法では、クラスター内のサンプルの重心(平均)と、そのクラスター内のサンプルとの距離の二乗和に基づいて、2つのクラスターを結合するかどうか決めます。
生田:どういうときにクラスターを結合するんですか?
応化:まず、すべてのクラスター内で、上の二乗和を計算しておきます。次に、ある2つのクラスターに着目します。2つの二乗和をAとBとします。2つのクラスターを結合したときに、そのクラスターにおいて同じく二乗和を計算します。これをABとします。すると、AB-A-Bを計算できますね。
生田:クラスターが2つあれば、計算は大変そうですが、計算できそうです。
応化:この計算をすべての2つのクラスターの組み合わせで計算して、AB-A-Bが最も小さいクラスター結合を、実際に採用して結合します。
生田:AB-A-Bが小さいっていうのは、どういう意味なんですか?
応化:AとBは各クラスター内のばらつきを表します。ABは結合した後のクラスター内のばらつきですね。
生田:はい。
応化:なので、AB-A-Bが小さいということは、結合前後でクラスター内のばらつきが変わらない、つまり統合しても同じような塊(クラスター)になるってことです。
生田:たしかに、互いに離れたクラスターA・Bが結合すると、ABは大きくなるので、AB-A-Bは大きくなりそう。
応化:そういうことです。近くにあって、なおかつばらつき具合が同じようなクラスターが結合しやすいんです。
生田:ウォード法が一番使われるんですよね?
応化:そうです。計算量は多いですが、妥当なクラスタリングの結果を得られやすい、と言われています。
生田:ウォード法でも、距離を計算するときに、いろいろな距離や類似度を非類似度に変換したものが使えますか?
応化:はい、もちろんです。
生田:了解です。とりあえずウォード法から計算してみます!
応化:それがよいと思います。PythonにもMATLABにもRにも、階層的クラスタリング用の便利なパッケージ・ライブラリがありますので、利用するとよいでしょう。
生田:わかりました、ありがとうございます!
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。