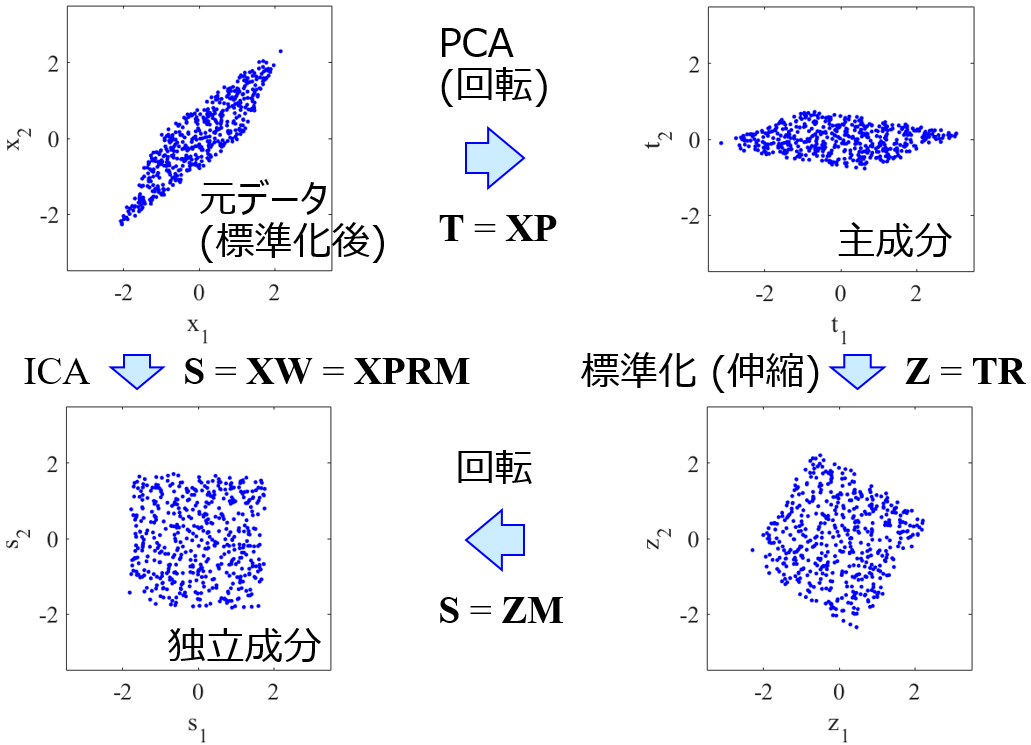
よく、主成分分析(Principal Component Analysis, PCA) と比べられることが多い、独立成分分析 (Independent Component Analysis, ICA) についてです。

PCA ではデータを低次元化したり、互いに無相関な成分を計算したりします。ICAでもデータの低次元化をしますが、ICAでは互いに独立な成分を計算できます。そして、独立というのは、無相関より強力なのです。ICA はスペクトル解析・信号処理・プロセス管理で使われることが多いです。データセットから、互いに関連の無い変数・成分を計算したいときは、ぜひご活用ください。

ICA のpdfファイルはこちらから、パワーポイント(pptx)ファイルはこちらからダウンロードできます。

pdfもスライドも自由にご利用ください。

興味のある方はぜひ参考にしていただき、どこかで使いたい方は遠慮なくご利用ください。

ICA の概要

• 主成分分析 (Principal Component Analysis, PCA) は、説明変数 X から互いに無相関な成分 (主成分) を計算する手法
• 主成分は、寄与率の大きい順に並べることが可能
  独立成分分析 (Independent Component Analysis, ICA) は、説明変数 X から互いに独立な成分 (独立成分) を計算する手法
• 独立成分は、どれも平等
• 独立は無相関より強力
• データセット内に外れ値があると、外れ値が強調されたような独立成分が抽出される

スライドのタイトル

• 独立成分分析 (ICA) とは？
• ICAの図解
• 無相関な変数 (成分) [数学的には p.25]
• 独立な変数 (成分) [数学的には p.25]
• 無相関と独立 [数学的には p.26, 27]
• ICAの問題設定 1/2
• ICAの問題設定 2/2
• 前処理としての主成分分析 (PCA)
• PCA を行うとどうなる？
• 前処理を2次元の図で表す
• ４次キュムラント
• ４次キュムラントの例
• 4次キュムラントの性質
• 4次キュムラントを最大もしくは最小にしてみる
• 4次キュムラントと独立性 式変形
• 4次キュムラントと独立性 性質
• 4次キュムラントと独立性 微分
• 4次キュムラントと独立性
• 独立成分の計算
• Lagrangeの未定乗数法
• w の決め方～不動点法～
• 不動点法のアルゴリズム
• 次の独立成分を計算する
• [参考] 数学的なこと
• [参考] 数学的な無相関・独立な変数
• [参考] 数学的な無相関と独立の関係
• [参考] 数学的な無相関と独立の関係
• [参考] 独立性の指標

以上です。

質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。