分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
y が目標値となる x もしくはそれに関連する化学構造などを設計することは、モデルの逆解析です。


モデルには線形モデルや非線形モデルがあり、x に制約がない場合もあれば制約がある場合もあります。化学構造などから x への変換が必要になる場合も。。。
そこでここでは、モデルの逆解析について整理します。
まずは線形モデルについて考えます。例えば、以下のようなモデルがあったとします。
y = 5x1 – 2x2
y の値の目標値が、例えば 10 と定められた場合、これを満たす x1 と x2 の組み合わせを求めることが、モデルの逆解析の対象です。
x に制約がない場合は、(x1, x2) = (0, –5), (2, 0), (4, 15), ・・・ などのように、無数に解析解が存在します。このように線形モデルで x に制約がない時に無数に解析解が得られることは、x の数が 3 以上になっても同様です。もちろん、x に制約がある場合は解が存在しないこともあります。モデルが線形であれば、制約がない場合も一般的な制約がある場合も、x の解が複数ではありますが線形計画法で x の解析解が得られます。
モデルが非線形モデルの時は、一般的には x の解析解を得ることができません。そのため、疑似的に逆解析を行うことになります。具体的には、まず x の候補を大量に生成します。x に制約がある場合は、その制約を満たした上で、候補を大量に生成します。その後、生成された x の候補を非線形モデルに入力して y の値を予測します。ベイズ最適化の場合には、予測値だけでなくその分散を用いて獲得関数を計算します。y の予測値が良好な値を持つ候補や獲得関数の値の大きい候補を選択することで、y の目標値から x の候補が得られます。このように、非線形モデルに対しては、x から y の予測である順解析を繰り返す、擬似的な逆解析になります。
一方で、直接的逆解析では、

非線形モデルに対しても、モデルの形式は限定されますが、y の値から直接、x の値を予測できます。x に制約がある場合は、制約の範囲内で x の解が求られます。
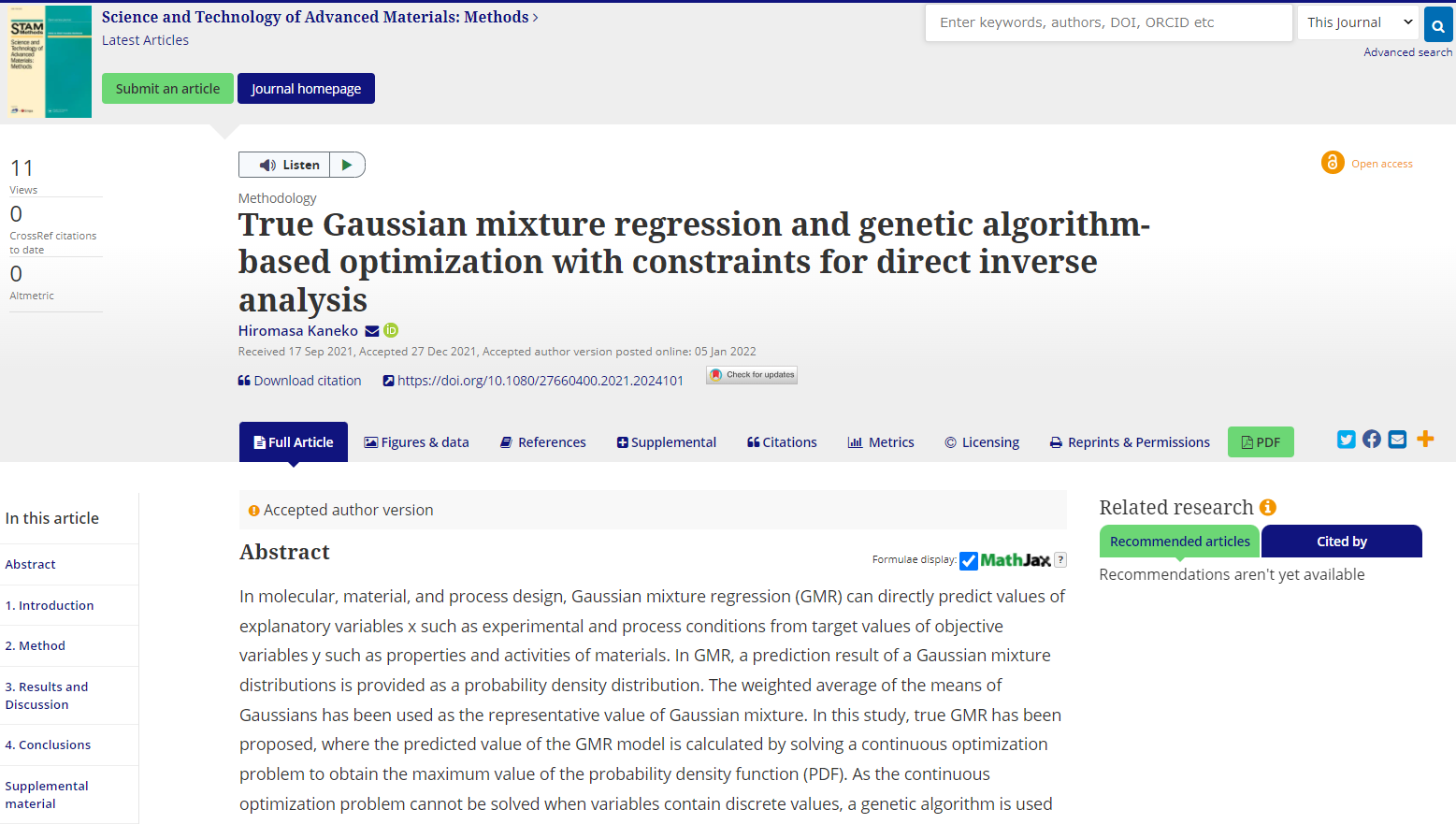
設計するものが数値で表現される x ではなく、化学構造など数値で表現されない情報の場合は、一般的には、化学情報から x への変換を挟む必要があります。その場合には、化学構造などを生成して、それを x に変換して、モデルを用いて x から y を予測する、擬似的な逆解析になってしまいます。
もし直接的逆解析をしたい場合には、こちらの方法を活用できます。
この方法では、非線形ニューラルネットワークの一種であるオートエンコーダを活用することで、化学構造から x となる潜在変数 (数値データ) への変換だけでなく、x から化学構造への変換を直接することができるため、y の目標値から直接的に化学構造を得られます。
分子・材料・プロセスの設計において、ぜひモデルの逆解析を活用しましょう。
以上です。
質問やコメントなどありましたら、X, facebook, メールなどでご連絡いただけるとうれしいです。


