金子研の論文が Science and Technology of Advanced Materials: Methods に掲載されましたので、ご紹介します。タイトルは
です。
分子や材料やプロセスのデータを用いて、説明変数 (分子記述子・合成条件・製造条件・プロセス条件など) x と目的変数 (物性・活性・特性など) y の間で数理モデル y = f(x) を構築し、構築されたモデルに基づいて、望ましい分子や材料やプロセスを設計します。x の値から y の値を予測することをモデルの順解析と呼び、逆に y の値から x の値を予測することをモデルの逆解析と呼びます。分子設計、材料設計、プロセス設計はモデルの逆解析に相当します。
一般的な逆解析で行われていることは、x のサンプルを大量に生成し、それらをモデルに入力することで y の値を予測し、予測値の中から適切なサンプルを選択することです。言い換えると、順解析を繰り返し行う擬似的な逆解析といえます。適応的実験計画法におけるベイズ最適化も、予測値が獲得関数の値に変わるだけで擬似的な逆解析であることは同じです。

一方で、Gaussian Mixture Regression (GMR) や Generative Topographic Mapping Regression (GTMR) によって構築された数理モデルでは、擬似的ではなく直接的に逆解析する、すなわち y の値から x の値を直接予測できます。
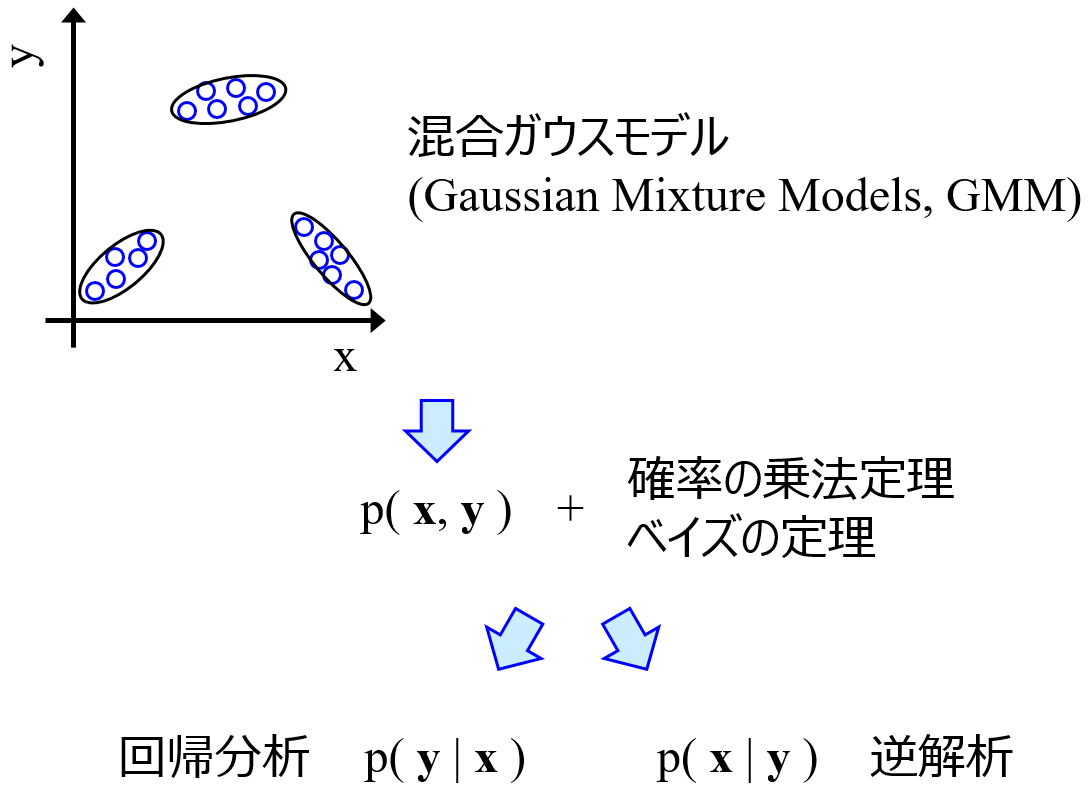

当研究室で開発している直接的逆解析法です。
GMR やGTMR により構築されたモデルでは、x と y の間のすべての関係、すなわち同時確率密度分布が複数の正規分布の重ね合わせで表現されます。この同時確率密度分布に基づいて、確率の乗法定理とベイズの定理により、y の値が与えられたときの事後確率密度分布を計算でき、x の確率密度分布を獲得でき、この分布も混合正規分布で表現されます。GMR による直接的逆解析法により、適応的実験計画法においてベイズ最適化を上回る効率化が達成されました。
さらに GMR におけるパラメータ最適化に、expectation-maximization (EM) algorithm だけでなく変分ベイズ法を用いることで、予測精度の向上を達成しました。
GMR や GTMR は y が複数の場合も対応でき、GTMR ではデータの可視化もモデルの順解析や逆解析と同時にできます。
GMR や GTMR においては、x と y が特徴量として平等に扱われるため、y から x の予測と x から y の予測が同じ方法で行われます。x から y を予測する時も、y から x を予測するときも、それぞれ y や x の確率密度分布として混合正規分布で表現されます。このあと、本来すべきことは、その確率密度分布、すなわち混合正規分布の値が最も高くなる y の値や x の値を、それぞれの予測値とすることです。しかし、実際行われていることは、あくまで簡易的に、各正規分布の平均値のなかで最も重みの大きい平均値を予測値としたり、各正規分布の平均値を各正規分布の重みを用いて重み付け平均した値を予測値としたりしています。この予測値が、確率密度分布の頂点、すなわち確率密度分布の最大値であるとは限りません。
そこで本研究では、GMR による x や y の予測値を、確率密度分布の値が最大になるように探索することを True GMR として提案しました。混合正規分布で与えられる確率密度関数を非線形関数として、非線形最適化問題を解きます。これにより、順解析においては x から y を予測するときに GMR の本来の確率密度分布の値が大きくなる y の値とすることができ、逆解析においては、y の目標値を達成する確率が最も高い x の値を予測できます。
また、モデルの逆解析においては、x に制約条件が存在する場合があります。例えばモル分率は 各成分の総和が 1 になる必要があります。また装置の耐久性や安全性によって、温度や圧力の上限や下限も存在します。添加剤の有無やいくつかの添加剤の組み合わせなど、実験条件によっては離散的な値をもつ x も考えられます。制約条件が上限・下限のみであったり、線形方程式や非線形方程式で表現できたりすれば、上述した非線形最適化問題で解けますが、特に離散的な特徴量があるときに、非線形最適化問題を解析的に解けません。そこで本研究では、メタヒューリスティクスアルゴリズム、特に遺伝的アルゴリズム (Genetic Algorithm, GA) を活用して、確率密度関数の値が高い x や y を探索する手法を提案します。GA において、制約条件を満たすように染色体を準備して、目的関数を確率密度関数とすることで、確率密度関数の値が高くかつ制約条件を満たす x を探索できます。本手法をGA-based Optimization with Constraints using GMR (GAOC-GMR) と呼びます。
以上のように、本論文では True GMR と GAOC-GMR を提案しました。これにより、x に連続値の特徴量しかないときに最適な解を求められたり、x に離散値の特徴量を含んだり複雑な制約条件があったりするときにも y の値から x の値を設計できたりします。今回は x と y の間の複雑な非線形関数を用いて、提案手法の検証をしました。GMR モデルを構築した後に、従来の方法で求めた x の値と、非線形最適化問題で求められた x の値や GA で探索した x の値における確率密度関数の値を比較することで、本手法により有意な x の値を設計可能であることを確認しました。さらに、GAOC-GMR を用いた最適化により、様々な制約がある場合においても、y の値が外挿領域にある場合においても、安定的に確率密度分布の高い値を探索できることを確認しました。
最後に、実際の超伝導体のデータセットや熱電変換材料のデータセットを用いて、効果的に直接的逆解析を行えることを検証しました。本手法は、分子設計、材料設計、プロセス設計などにおけるすべての逆解析に活用できます。
興味のある方は、ぜひ論文をご覧いただければと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。