
金子研の論文が ACS Omega に掲載されましたので、ご紹介します。タイトルは
Integration of Materials and Process Informatics: Metal Oxide and Process Design for CO2 Reduction
です。これは修士卒の岩間稜さんが修士2年生のときに取り組んだ研究の成果です。CO2 から一酸化炭素 (CO) を生成する reverse water gas shift chemical looping (RWGS-CL) 反応およびそれを実現する RWGS-CL プロセスを対象にして、マテリアルズインフォマティクスとプロセスインフォマティックスを融合した、材料の合成条件と製品のプロセス条件を同時に設計する手法に関する論文です。
RWGS-CL 反応は、金属酸化物を酸素キャリアとして、reverse water gas shift (RWGS) 反応を 2 つの半反応に、時間的に分離することで進行します。これまで、高い CO2 転化率と H2 転化率をあわせもつ金属酸化物や担体の探索や、その合成条件やプロセス条件の探索が行われていました。しかし、目標の特性をもつ金属酸化物・担体・合成条件の設計と、目標のプロセスとなるプロセス条件の設計は、それぞれ個別に行われており、例えば金属酸化物を設計するときはプロセスに関する情報が考慮されてなく、逆にプロセスを設計するときは金属酸化物に関する情報が考慮されていません。その結果、それぞれの観点から見ると有望な合成条件やプロセス条件が見落とされている可能性がありました。
本研究では、CO2 転化率・H2 転化率ともに高い金属酸化物とその合成条件、そして実際の装置におけるプロセス条件を同時に最適化することを目的とし、金属酸化物の設計とプロセス設計を融合します。合成条件や金属酸化物の特徴量を x とし、実験結果である CO2転化率・H2 転化率を y とする数理モデル y = f(x) と、その数理モデルの予測結果と RWGS-CL プロセスにおけるプロセス条件を x、目的のプロセス要件を y とした数理モデル y = g(x) の両方を活用します。さらに、ベイズ最適化や直接的逆解析により新たな金属酸化物およびプロセス条件を提案します。

そのため回帰モデル構築手法として Gaussian Process Regression (GPR) と Gaussian Mixture Regression (GMR) を検討しました。

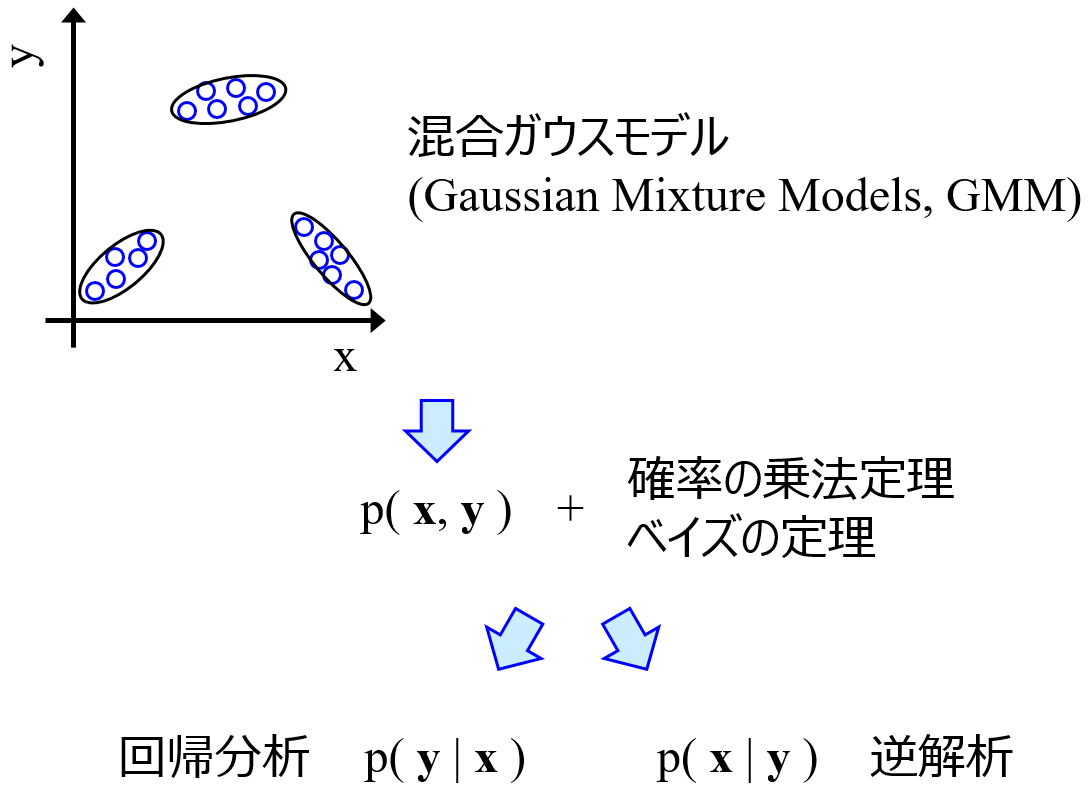
GPR モデルでは、シミュレーション結果が未知の x を入力することで、y の予測値だけでなくその分散を推定できます。推定結果から、目標のプロセス要件を達成する確率が高い x の値を選択します。GMR モデルでは、y の目標値をモデルに入力することで x の値を直接的に予測できます。この直接的逆解析を利用して x の値を選択します。このように機械学習を活用して選択された x の値でプロセスシミュレーションを行うことにより、少ないプロセスシミュレーション回数で目標のプロセス要件を満たす x の値を探索に成功しました。
興味のある方は、ぜひ論文をご覧いただければと思います。どうぞよろしくお願いいたします。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


