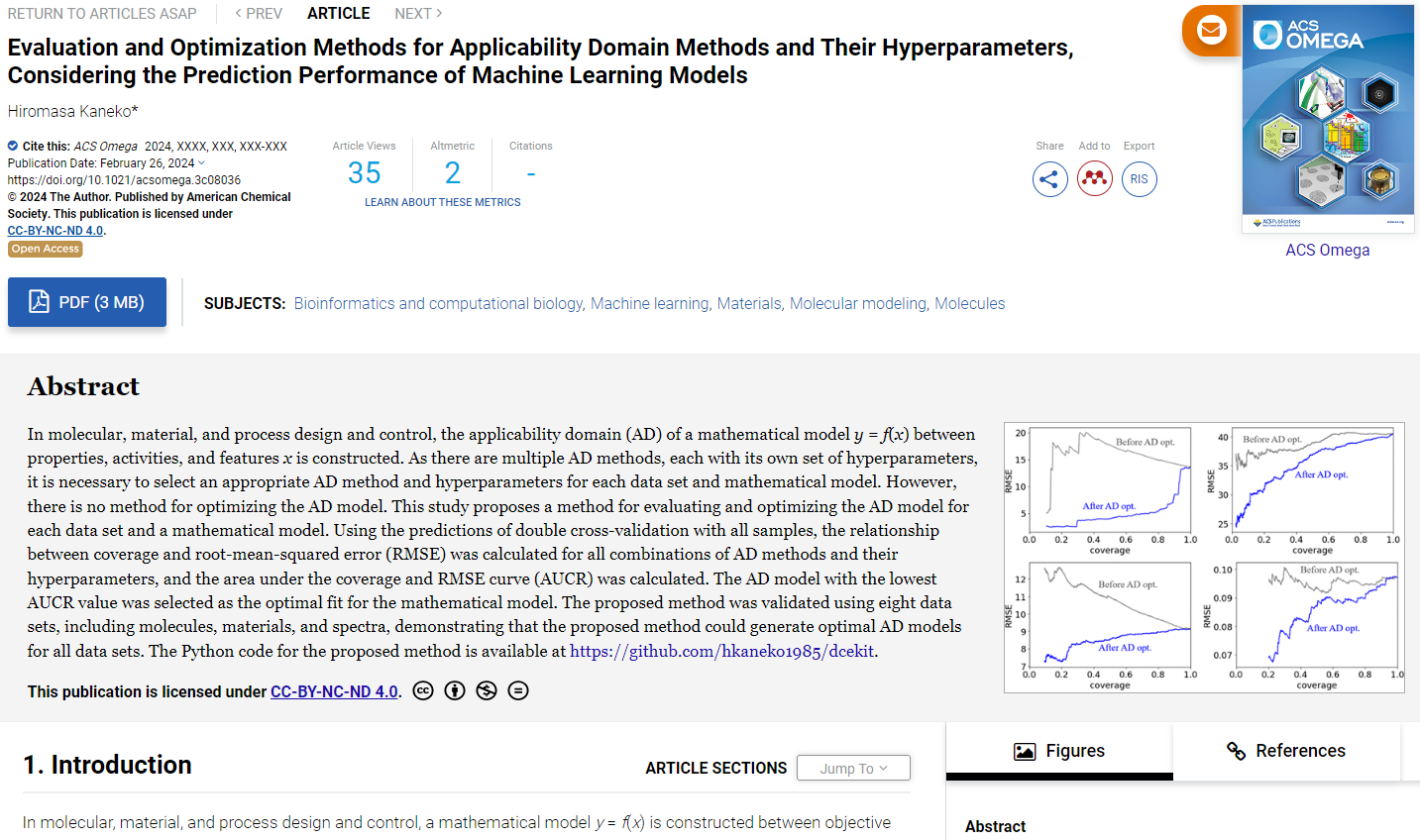
金子研の論文が ACS Omega に掲載されましたので、ご紹介します。タイトルは
です。
分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築します。構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
予測精度の高いモデルを構築することが重要ですが、一方で、サンプル数やその内容によって、モデルを適用できるデータ領域が異なります。少数しかサンプルがなければ、その周辺のごく小さなデータ領域しか的確には予測できませんが、サンプル数が増えることでそのようなデータ領域は広がります。このデータ領域をモデルの適用範囲 (Applicability Domain, AD) と呼びます。


特にモデル構築用サンプルが少数の場合、新たなサンプルの y の値を予測したときに、実際は AD の外のため予測値を信頼できないにもかかわらず、AD を設定していないためそれに気づかず、誤って予測値を信頼してしまう危険があります。モデルを構築した後は、その AD を設定する必要があります。
AD の設定するための様々な手法があり、さらに手法ごとにハイパーパラメータがあります。データセットごとに、AD の設定手法およびそのハイパーパラメータを最適化することが望まれますが、AD の設定は教師なし学習であるため、AD だけではデータセットごとの最適な AD を設計することはできません。
本論文では、モデルの予測性能を考慮することで、AD の設定手法およびそのハイパーパラメータを最適化する手法を提案しました。ダブルクロスバリデーションにより、

y の予測値を計算し、その予測値に基づいて AD の設定手法およびそのハイパーパラメータごとに、coverage と RMSE (Root-Mean-Square Error) もしくは MAE (Mean Absolute Error) との関係を求めます。その関係が良好な結果となるような AD の設定手法およびそのハイパーパラメータを選択します。
実際の分子や材料のデータセットを用いて、提案手法を検証しました。様々な回帰分析手法の中からモデルの予測性能に基づいてデータセットごとに最適な回帰分析手法を選択した後に、AD の設定手法およびそのハイパーパラメータを提案手法により最適化できることを確認しました。
興味のある方は、ぜひ論文をご覧いただければと思います。どうぞよろしくお願いいたします。
以上です。
質問やコメントなどありましたら、X、facebook、メールなどでご連絡いただけるとうれしいです。