説明変数 x のデータを準備して、低次元化やクラスタリングによりデータセットの可視化や解釈をしたり、x と目的変数 y のデータを揃えて回帰分析やクラス分類をしたりするときに、データセットの前処理の一つとして、基本的に特徴量の標準化 (オートスケーリング) を行います。

基本的には、特徴量ごとに、その平均を引いて標準偏差で割る、標準的な操作をすればよいのですが、場合によっては、データ解析・機械学習の目的によっては、少し工夫をした方がよいときもあります。このあたりの工夫について、整理しながら説明します。
決定木やランダムフォレストのとき、オートスケーリングは不要
いきなりオートスケーリングを「しない」話で恐縮ですが、決定木やランダムフォレストをするときはオートスケーリングをする必要はありません。
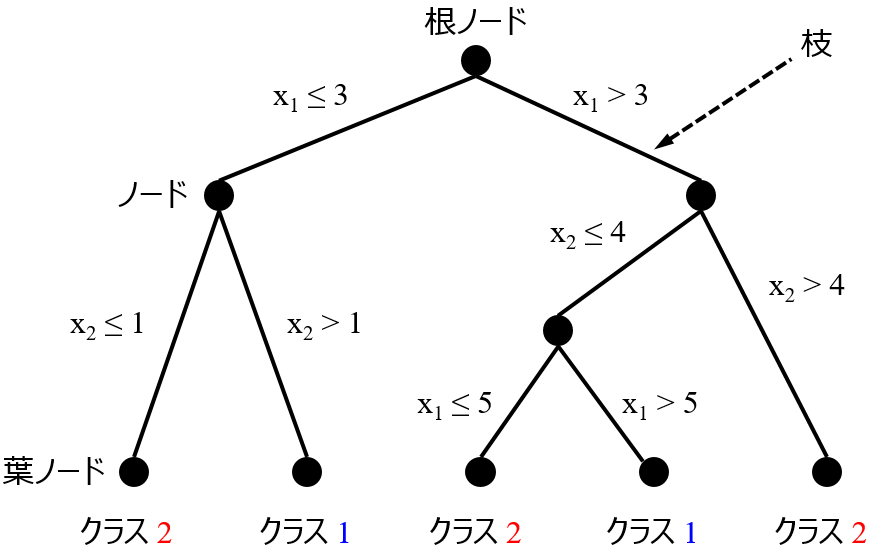
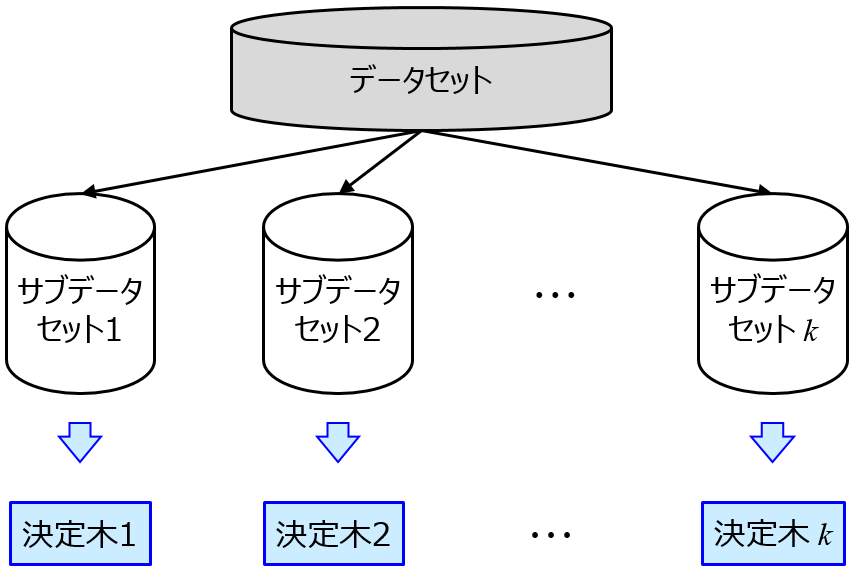
決定木では、x の閾値や y の平均値のみが扱われますので、オートスケーリングは不要です。オートスケーリングせずに生の値を用いることで、決定木を解釈しやすくなるといったメリットもあります。決定木をアンサンブル学習させるランダムフォレストも同様に、オートスケーリングをしなくて大丈夫です。ランダムフォレストにおいて特徴量の重要度を計算するときも、オートスケーリングをしてもしなくても結果に影響はありません (計算方法によっては重要度の値が変わることもありますが、そもそも絶対値に意味はなく比較するための指標なので気にしなくて OK です)。
ただ、ブースティングのような、モデルの誤差に基づいて次のモデルを構築するようなときは、モデルの誤差をどのように次のモデルに引き継ぐかのハイパーパラメータが存在することもあり、x のオートスケーリングは不要ですが、y はオートスケーリングしたほうがよいです。これにより標準化したあとの y の誤差 (標準化されたあとの誤差) になるため、一般的なハイパーパラメータの値や候補群を使用できます。
線形モデルのときは、少なくともセンタリングをする
線形モデルを構築するとき、基本的にデータセットの回転をします。回転する中心が原点、つまり平均が 0 でないと、効果的に回転できないため、スケーリングの有無はさておき、センタリングは必ず行うようにしましょう。
同じ意味の特徴量をまとめてスケーリングする
まったく同じではありませんが、特徴量の種類が同じだったり、同じ意味をもつ特徴量を一緒に扱ったりするときの話です。例えば、スペクトルのデータを他のプロセス変数やプロセス条件のデータと一緒に扱うことを考えます。一般的には、スペクトルの波長や波数ごとに、平均値と標準偏差を計算して、それぞれ引いたり割ったりしますが、標準偏差を波長や波数ごとではなく、スペクトル全体で一つ計算します。線形モデルの話のときに出たように、特徴量ごとの平均値は 0 にする必要があるため、センタリングは普通に実施します。一方でスケーリングは、スペクトル全体 (行列全体) で一つの標準偏差を計算して、スペクトル全体をその標準偏差で割ります。波長や波数ごとにばらつきばらつきが異なるなかで、そのばらつき具合が重要なとき、一般的なスケーリングではすべての波長や波数で標準偏差が 1 になってしまい、ばらつき具合を評価できませんが、スペクトル全体で標準偏差を統一にすることで、波長や波数ごとのばらつきを考慮した上でモデリングできるようになります。もちろん、スペクトルのデータ以外のプロセス変数やプロセス条件のデータともスケールを合わせた上で解析できます。
スペクトルのデータだけでなく、いろいろな箇所で測定された温度や圧力などの同じ意味をもつプロセス変数において標準偏差を計算してスケーリングした方がよいかもしれません。このあたりは、データ解析・機械学習の目的に応じて決めるとよいでしょう。
転移学習のときのように、0 に意味がないときときは 0 以外で平均や標準偏差を計算する
ゼロ行列を活用するタイプの転移学習のとき、ゼロ行列以外のサンプルで平均や標準偏差を計算してオートスケーリングを行います。

それ以外でも、いろいろな実験方法で合成されたサンプルが混在しているときなど、実験方法の違いを表現するために、実験方法ごとのパラメータにおいて、該当しない実験方法のサンプルの値を 0 にするときがあります。このとき、オートスケーリングを行う際は、0 を含めて平均や標準偏差を計算するのではなく、0 以外の値で平均や標準偏差を計算したほうが、的確に平均や標準偏差を考慮できます。
それぞれオートスケーリングする際のちょっとした工夫ですが、データ解析・機械学習をする目的に応じて、適切に使い分けるとよいと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


