線形のクラス分類モデル・回帰分析モデルでは、説明変数 (記述子・特徴量) ごとに重みが求まります。実際には説明変数の間には相関関係があるためモデルの解釈は簡単ではありませんが、重みを見ることでそのモデルを解釈した気になれます。

ただ、非線形のモデルでは重みすら求まりません。今回はそんなときに、モデルを各説明変数で偏微分しよう！というお話です。モデルの微分で何ができるか、具体的な微分の計算方法などが説明されています。pdfもスライドも自由にご利用ください。

pdfファイルはこちらから、パワーポイント(pptx)ファイルはこちらからダウンロードできます。

興味のある方はぜひ参考にしていただき、どこかで使いたい方は遠慮なくご利用ください。

モデルの微分による非線形モデルの解釈

線形モデル
- 標準回帰係数などの重みを見ることで、各説明変数 (記述子・特徴量) の重みを検討できる
非線形モデル
- モデルを各説明変数で偏微分
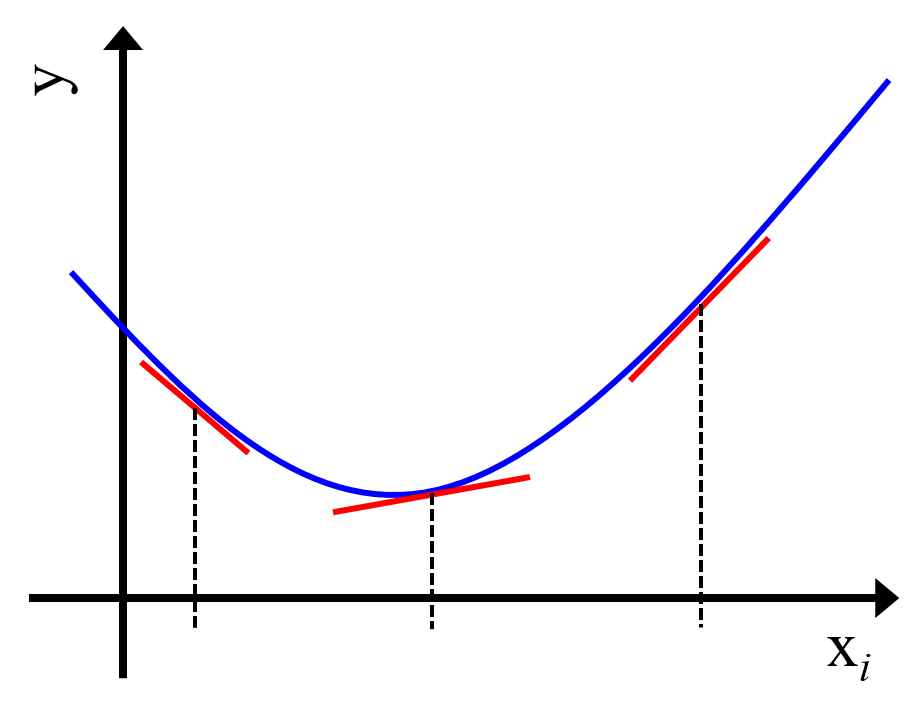
- 説明変数空間におけるある点 (たとえば、あるサンプル) における微分係数を計算することで、その点における説明変数ごとの傾きを計算できる
- 傾きが大きいということは、その点において値を変化させることで、目的変数の値の変化も大きい説明変数であるということ