回帰分析やクラス分類によって構築された、目的変数 Y と説明変数 X との間のモデル Y = f(X) についてです。
モデルについて議論するとき、モデルはデータの外挿は予測できない、内挿しか予測できない、とか、その予測結果は内挿なの?外挿なの?、とかの話があると思います。一方で、モデルの適用範囲・適用領域 (Applicability Domain, AD) という概念があります。モデルの適用範囲は、モデルがトレーニングデータにおける予測精度と同様の精度で予測できるようなデータ領域のことです。詳しくはこちらをご覧ください。

今回は、内挿・外挿と、モデルの適用範囲内・適用範囲外との違いについてお話しします。
まず、内挿の Wikipedia には次のように書かれています。
内挿(ないそう、英: interpolation)や補間(ほかん)とは、ある既知の数値データ列を基にして、そのデータ列の各区間の範囲内を埋める数値を求めること、またはそのような関数を与えること。またその手法を内挿法(英: interpolation method)や補間法という。対義語は外挿や補外。内挿するためには、各区間の範囲内で成り立つと期待される関数と境界での振舞い(境界条件)を決めることが必要である。
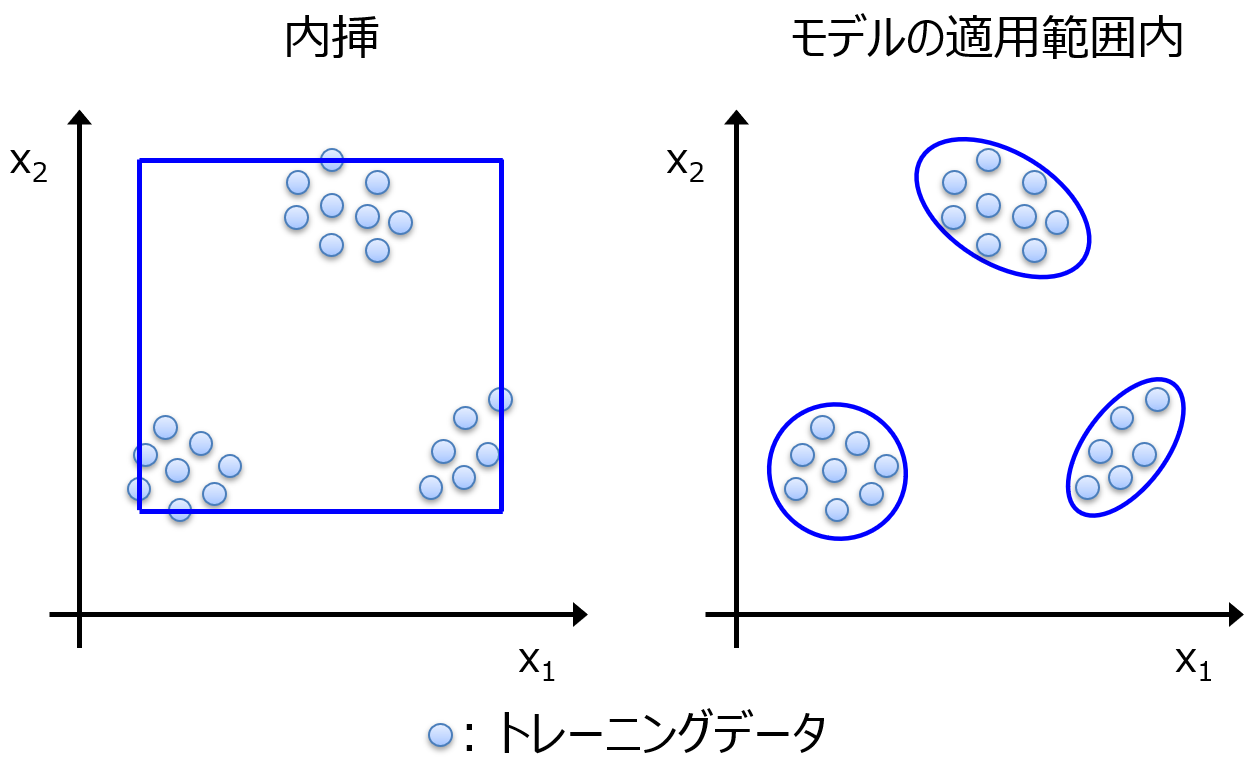
つまり、各説明変数 x の最小値から最大値までが内挿というわけです。図で表すと、以下の青線の四角形の中が内挿になります。
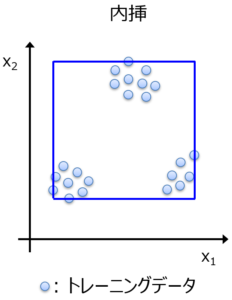
図では説明変数が x1, x2 の 2 つ場合に、x1, x2 ともに最小値と最大値の中に入る範囲を示しています。どんな説明変数も、最小値を下回ったり、最大値を上回ったりすることがありません。x1 と x2 とで独立して範囲が決められています。いずれかの説明変数で、最小値を下回ったり、最大値を上回ったりすれば、それは外挿となります。そのため、「モデルは外挿を予測できない」 ということは、1 つの説明変数でも、その最小値を下回ったり、最大値を上回ったりすると、そのサンプルは予測できない、と同じ意味になります。
一方で、上の図ではデータの分布が 3 つに分かれている、つまりサンプルが 3 つの集団に分かれているように見えまして、それらの集団の間にある、サンプルのない空白地帯は、内挿になっています。「モデルは内挿しか予測できない」 ということは、すべての説明変数で最小値を下回ったり、最大値を上回ったりすることがなければ、仮にトレーニングデータのない空白地帯にあるサンプルでも、そのサンプルは予測できる、と同じ意味になりますが、本当にこのような空白地帯のサンプルも予測できるか、あやしいです。
次にモデルの適用範囲です。もちろん上図の内挿のようにモデルの適用範囲を設定することもできますが、一般的に用いられている方法は、下図のようにデータ密度によってモデルの適用範囲を設定する方法です。
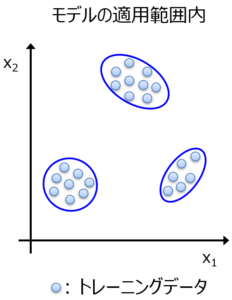
これらの青線の円の中の領域が、モデルの適用範囲内となります。内挿の図と、モデルの適用範囲の図を比べると、たとえばモデルの適用範囲では、空白地帯が少ないことがわかります。トレーニングデータに近い領域が、モデルの適用範囲となっています。内挿における空白地帯は、モデルの適用範囲外であり、トレーニングデータと同じ精度では予測できない可能性がある、と判断されます。
一方で、外挿でもモデルの適用範囲内となる領域はあります。上図において、x1 や x2 の最小値を下回ったり、最大値を上回ったりしていても、青線の円の中の領域があることを確認できます。朗報としては、あるサンプルが外挿でも、モデルの適用範囲であればトレーニングデータと同様の予測精度でそのサンプルを予測できます。
構築したモデルを運用するときには、モデルの適用範囲を必ず設定し、内挿・外挿ではなく、モデルの適用範囲内・適用範囲外で議論するのがよいと考えています。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。