プロセス・マテリアルズ・ケモインフォマティクスオンラインサロン (金子研オンラインサロン) をやっていまして、
そこで興味深い質問があり、回答しました。今回は回答した内容を少し膨らませて、こちらの記事でもお話したいと思います。
材料設計やプロセス設計をするとき、説明変数 X と目的変数 Y との間でモデル Y = f(X) を構築した後、Y の目標値を達成できるような X の候補を探索するため、X の仮想的なサンプル候補をたくさん生成して、それらをモデルに入力して、Y の予測値を計算したり、ベイズ最適化であれば獲得関数の値を求めたりします。そして、それらの値が良好な X のサンプルを選びます。
もちろん Y の値が望ましい値になることは目的の一つですが、たとえば X の値を一つに決めても、実際に材料を作るときにその通りに制御することが難しいことや、製造する際に多少 X の値が変化しても Y の値が変わりにくいところを設定したいといったことはあると思います。そんなとき、設計した X の値で Y の値が目標を達成したとしても、X の値が少しずれるだけで Y の値が変わってしまうようでは困ってしまいます。
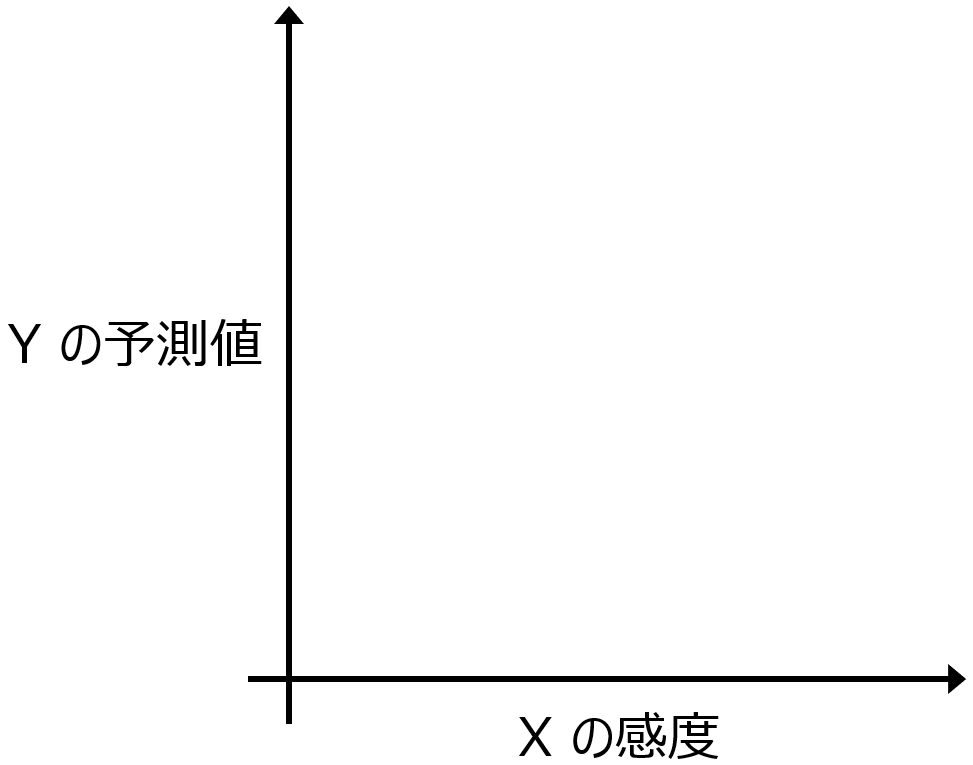
このような、Y の値だけでなく X の感度を考慮したモデルの逆解析についてお話しします。
仮想的にたくさん生成した X のサンプルをモデルに入力して Y の予測値や獲得関数の値を計算しますが、そのとき、サンプルそれぞれにおいて、その X の値からばらつきうる範囲で意図的に値を振ります。たとえば、100 サンプルを生成します。その 100 サンプルをモデルに入力して、予測値や獲得関数の値を計算して、その標準偏差の値を計算します。生成した仮想的なサンプルそれぞれに対して、Y の予測値もしくは獲得関数の値と、その標準偏差を計算するわけです。ここで計算される標準偏差は、アンサンブル学習法での標準偏差やガウス過程回帰での標準偏差とは異なるので注意してください。あくまで、ある X のサンプルの周りで多数生成した X のサンプルで計算された予測値もしくは獲得関数の値の標準偏差です。
この標準偏差の値が小さいということは、その X の値周辺で多少値が変化したとしても、Y の予測値もしくは獲得関数の値は変わりにくいことを意味します。逆に標準偏差が大きいということは、その X の値あたりで値が変わってしまうと Y の予測値や獲得関数の値も大きく変化してしまう可能性があるということです。
たとえば仮想的に生成された X のサンプルについて、Y の予測値とその標準偏差の値の関係を、下図のようにプロットして確認します。
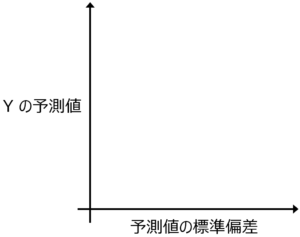
たとえば Y の予測値が大きく、かつ X の値の周辺における Y の予測値のばらつきが小さいような候補が欲しい場合は、プロットの左上にあるサンプルを選択すればよいと思います。
獲得関数の値が大きく、かつ X の値の周辺における獲得関数のばらつきが小さいような候補が欲しい場合は、下図の左上にあるサンプルがよいと思われます。
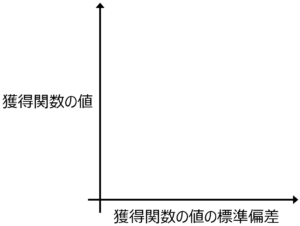
以上のようにすることで、Y の予測値や獲得関数の値が同じような値になったサンプルの中で、差別化できるともいえます。
また、Y の予測値や獲得関数の値が大きく、かつその標準偏差が大きいサンプルは、X の少しの違いによって物性や活性が大きく変化するということですので、興味深いサンプルと考えることもできるかもしれません。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。