説明変数 X と目的変数 Y の間で回帰モデル Y = f(X) を構築するとき、X と Y の間の関係は一貫している必要があります。下の図をご覧ください。
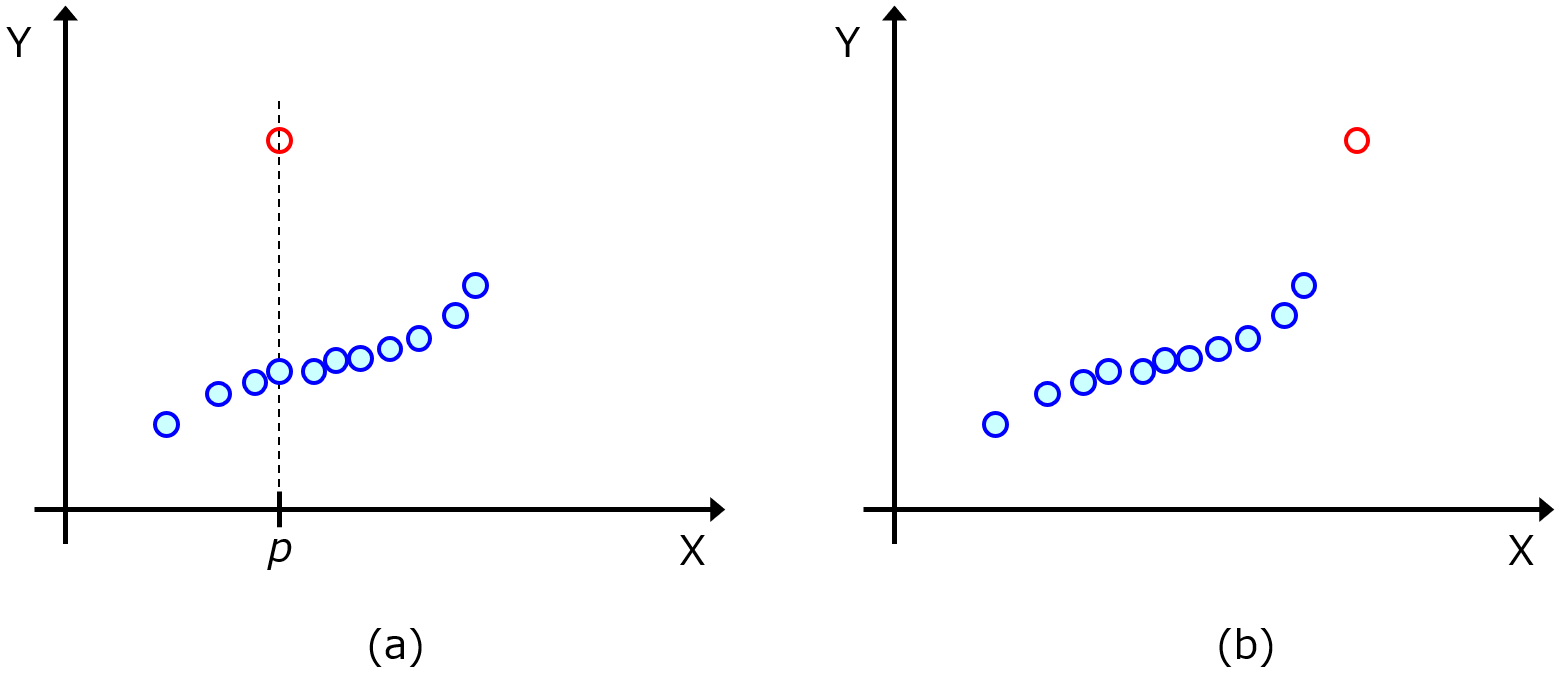
上の (a) の図では、X と Y の間の関係は一貫していません。X の値が p のときに、Y の値として 2通りの候補があります。この赤丸のようなサンプルは、回帰モデルを構築するときに、モデルの推定精度を下げる原因になります。一方で、上の (b) の図では、X と Y の間の関係は、一貫しています。曲線的で、非線形の関係ですが、ある一つの関係性をもって、X と Y の値が変化していることがわかります。回帰モデルを構築するときには、(b) の図のように X と Y の間の関係が一貫している必要があります。
上の (a) の図における赤丸のサンプルのように、いくつかの外れ値があるということでしたら、たとばこちらのような手法を使うことで外れ値を検出したり、
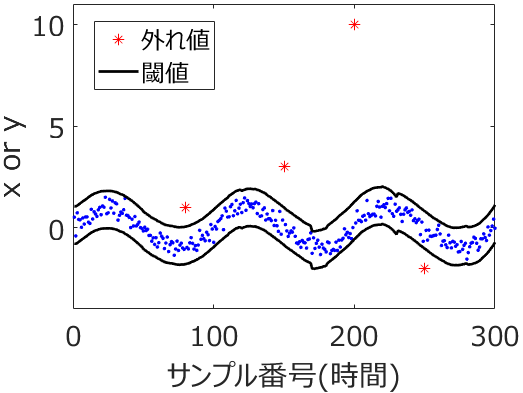
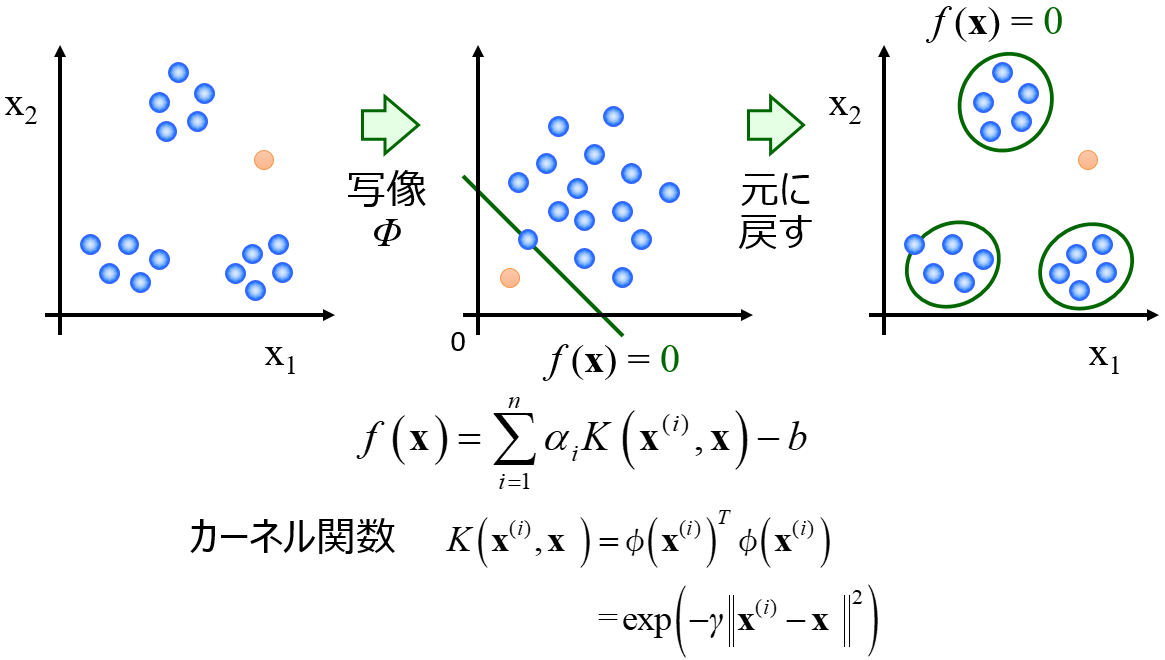

検出した外れ値に対してこちらの手法で値を補完することができます。

この記事でさらに考えることは、あるデータセット内において、X と Y の関係性が異なる複数の (サブ) データセットがあるような状況です。たとえば下の図のような状況です。
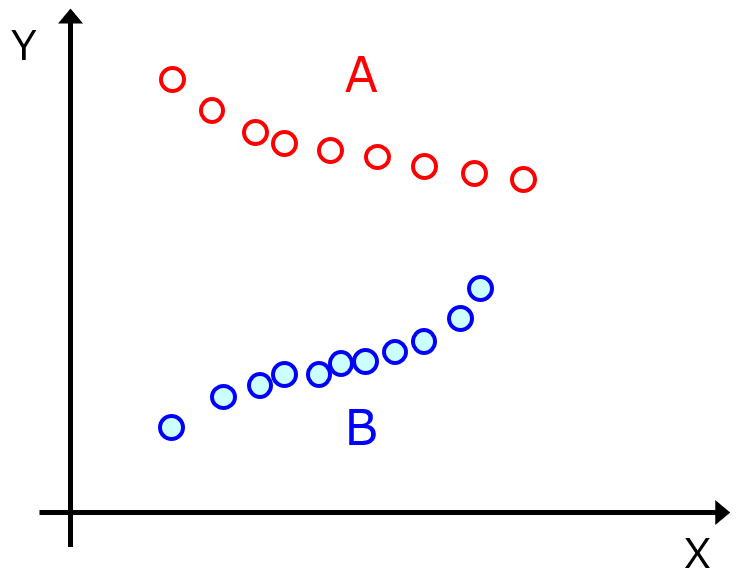
このような状況では、A のサンプル群だけ、B のサンプル群だけ、それぞれ取り出す必要があります。なお、今回は見やすいように、A を赤色で、B を青色で色分けしていますが、実際には (たとえばすべて黒色で) 色では見分けることができません。
上の図のように、X が一つ、Y が一つであれば、図示して A のサンプル群だけ、B のサンプル群だけを選ぶことはできますが、実際には X は複数ありますので、目で見て確認することができません。与えられたデータセットにおいて X と Y の関係が一貫しているサンプル群のみを取り出す必要があります。さらに、一つのサンプル群だけ取り出せばよいわけではなく、複数のサンプル群を取り出します。
図を見て分かる通り、X だけではサンプル群を分けることは不可能です。X と Y の関係性が一貫しているかどうかがカギになるので、Y を使用する必要があります。たとえば、X に変数として Y を追加してから、クラスタリングをすることで、上手くサンプル群を分けられるかもしれません。ただ、このクラスタリングにおいては、サンプル同士の類似度 (距離や相関など) に基づいて分けれれるだけで、X と Y の関係の一貫性については考慮されていません。
ちなみに、このようなデータセットの整理・作成は、ソフトセンサー解析、プロセス管理 (異常検出など) といった時系列データの解析で行われることが多いです。また、あるサンプルを考えたとき、複数のサンプル群 (サブデータセット) に含まれることを許容してもよいといえます。上の図において、A の一番右のサンプルなど、A に含まれ、かつ B にも含まれるようなサンプルがあってもよいということです。このような状況において、わたしは以下の手順でサブデータセットを作成します。
- 時間的に連続した、少数のデータセットを選択し、サブデータセットとする (たとえば 30 サンプル。このサンプルにおいては、X と Y の関係は一貫していると仮定)
- サブデータセットを用いて回帰モデルを構築する (基本的に非線形の手法で構築します)
- 次の時刻の X の値をモデルに入力して、Y の値を予測する
- Y の予測誤差の絶対値が、モデルを構築したデータセットでクロスバリデーションをしたときの予測誤差の標準偏差の 3 倍以内である場合、サブデータセットに追加して に移る。3 倍を超えた場合は終了する
あるサンプルをサブデータセットに追加するかどうかにおいて、Y の誤差が小さいということは X と Y の関係性が一貫しているということです。このようにして、30 サンプルから、一つずつサンプルを増やしながらサブデータセットを作成します。修了したら、最初の 30 サンプルの開始時刻を少しズラして、再度サブデータセットを作成します。ここでサンプルの重複を許すわけです。このようなサブデータセットの作成を繰り返します。
ご参考になれば幸いです。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。

