バッチプロセスにおいて、プロセスの異常を検出したり異常原因の診断をしたり、説明変数 X と目的変数 Y との間でモデル Y = f(X) を構築して X から Y を予測したり、Y が望ましい値になるようにバッチプロセスを設計したりすることがあります。そのときの特徴量の作り方についてお話しします。
特徴量の作り方の基本的な方針は、バッチプロセスにおいてデータ解析や機械学習で何をやりたいか、つまりデータ解析や機械学習の目的に依存します。たとえば、リアルタイムに異常検出や異常診断をしたり、Y の値を予測したりしたい場合、つまりバッチプロセスとはいえ連続プロセスと同じようなことをしたい場合は、バッチを意識する必要はありません。連続プロセスと同様にしてプロセス変数が特徴量になり、一つの時刻を一つのサンプルとして時刻ごとにプロセス変数の値を並べたものがデータセットになります。もちろんプロセスに動特性がありそのダイナミクスが重要なときは、時間遅れ変数を追加します。
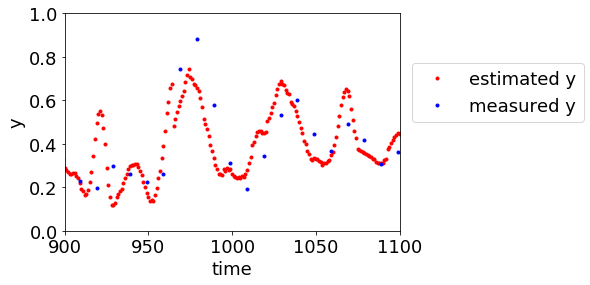
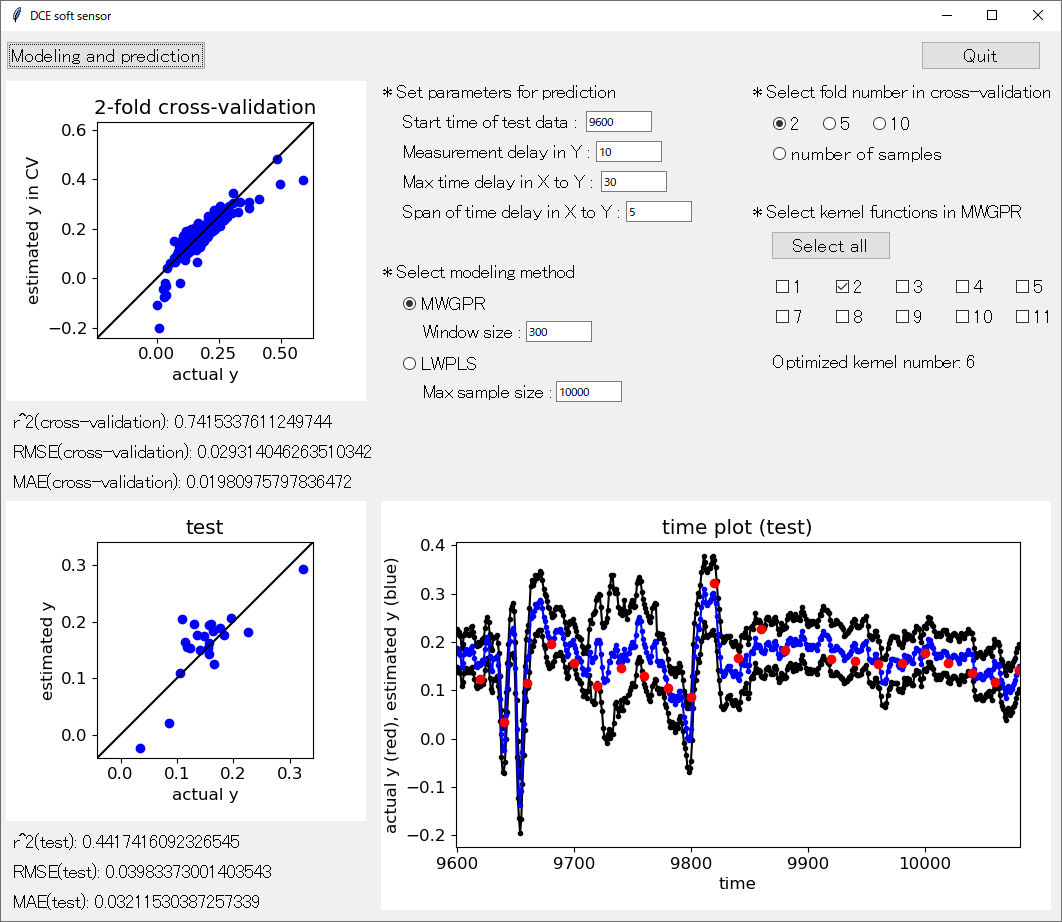
ここでバッチプロセスは連続プロセスと異なり、バッチごとにサンプルのグループが分かれているため、グループごとに時間遅れ変数を作成することに注意が必要です。
一方で、バッチプロセスの終点が Y となる場合は、1バッチが1サンプルになります。このときの特徴量の作り方として最も単純なのは、プロセス変数ごとに時間遅れ変数と同じようにして横にプロセス変数の時間変化を並べることです。プロセス変数の数が m 個、バッチごとの時刻 (サンプル数) が n 個のときは、特徴量の数が (m × n) 個になります。ただこのやり方では、バッチごとに1バッチの時間が異なるときに、サンプルごと (バッチごと) に特徴量がそろわなくなってしまいます。そのため、全バッチで特徴量の数、m の数が同じであれば n の数を合わせる必要があります。たとえば、バッチ時間が最も短いサンプルに時間を合わせて、それより長い時間のバッチはその時間分だけ削除することで合わせたり、バッチの時間が短いバッチに対して測定されていない分を直線などで補完して長い時間に合わせたりします。もしくは、バッチ時間が等しくなるようにバッチごとに時間軸を圧縮もしくは伸長して変更し、合わせることもあります。そのときにはスプライン補間などの補間手法が有効です。
他には、バッチの特徴量をプロセス変数ごとに統計量を計算することで作成します。たとえばバッチにおける特徴量の最大値、最小値、四分位数 (中央値など) や、平均値・標準偏差などの統計量です。そのうプロセスを考慮して、Y である終点に関係ありそうな統計量を考えて採用します。一つのバッチの中で、プロセスが分かれているとき (昇温プロセス、降温プロセス、昇圧プロセス、降圧プロセスなど) は、プロセスごとに計算することもあります。フーリエ解析やウェーブレット解析などで変換した後の特徴量を使用してもよいです。
以上のようにプロセスことに意味のある特徴量を検討するとよいでしょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


