回帰分析やクラス分類を行うとき、オーバーフィッティング(過学習)をしないことが重要といわれます。
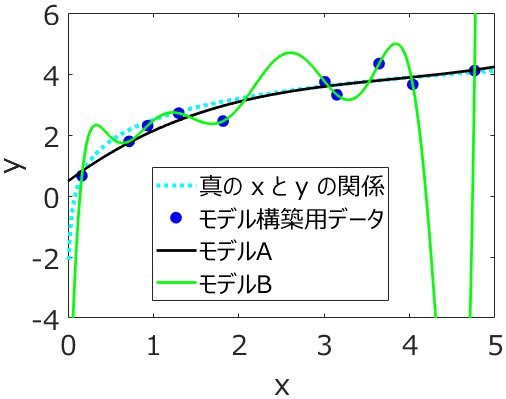
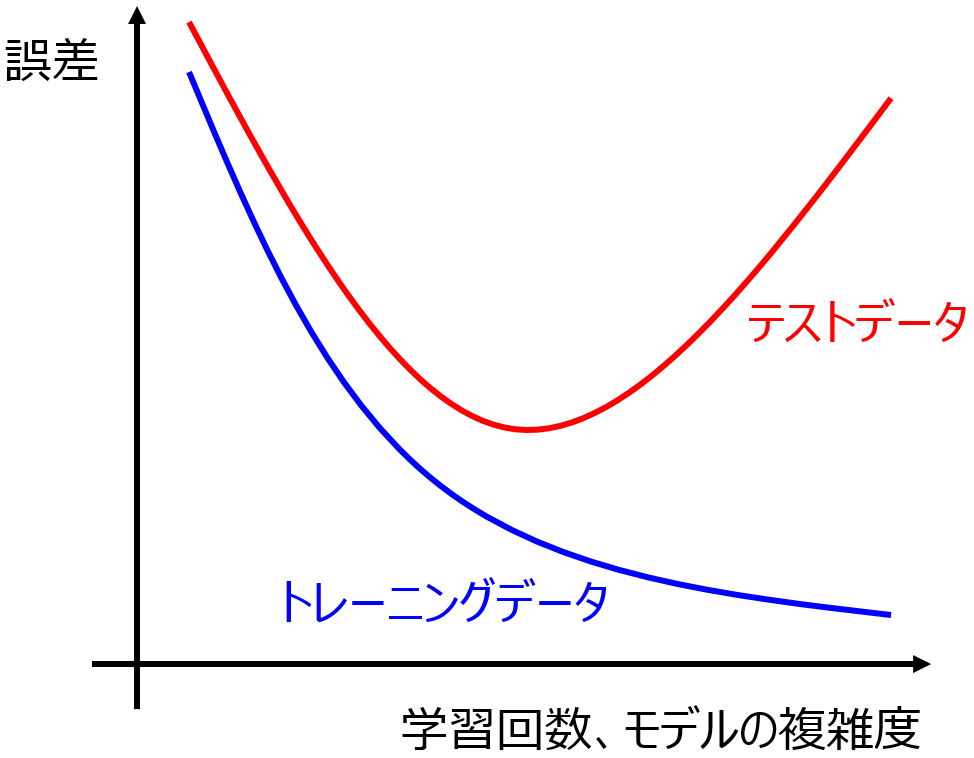
オーバーフィッティングを防ぐため、クロスバリデーションでハイパーパラメータを決めたり、テストデータを用いて回帰分析手法やクラス分類手法を選んだりします。

オーバーフィッティングの反対として、アンダーフィッティングがあります。アンダーフィッティングは、学習が十分に行われていなく、トレーニングデータにモデルが適合していない状態です。アンダーフィッティングやオーバーフィッティングを理解するため、k最近傍法が便利です。k=1 のときは (極端な) オーバーフィッティングに相当します。回帰係数やクラス分類においてトレーニングデータにおけるサンプルの予測結果は、それぞれ自分自身の目的変数の値やカテゴリーになります。回帰分析においてトレーニングデータにおける r2 は 1 になり、クラス分類において正解率は 100% になります。しかしテストデータなどの新しいサンプルを適切に予測できるかわかりません。
一方で、k を増やしていき、k = (トレーニングデータのサンプル数) とすると、(極端な) アンダーフィッティングに相当します。回帰係数やクラス分類においてトレーニングデータにおけるサンプルの予測結果は、それぞれトレーニングデータ全体の目的変数の平均値や多数決の結果になります。回帰分析においてトレーニングデータにおける r2 は 0 になり、クラス分類において正解率はカテゴリーの割合になります。このようなモデルにはまったく意味が全くありません。
オーバーフィッティングの問題として、モデルがノイズにも適合する、外れ値にも適合する、といったことが言われています。もちろん実際にそのようなことが起きているとは思いますが、具体的なノイズを取り出すことはできないため、本当にノイズに適合しているのか、(まだ) 適合していないのか、わかりません。テストデータで検証してはいますが、テストデータにもノイズが含まれているため、テストデータによく当てはまった分、よりノイズに適合していない、とはいえません。オーバーフィッティングやアンダーフィッティングを防ごうとしたときに、定性的な議論になってしまいます。
わたしは、オーバーフィッティングやアンダーフィッティングの問題を、モデルの適用範囲 (Applicability Domain, AD) の広さで考えています。

オーバーフィッティングしているということは、AD が狭いということです。AD はトレーニングデータにおいてモデルが発揮した予測精度であり、新たなサンプルを予測できるデータ領域です。オーバーフィッティングしているということは、トレーニングデータにおける予測精度は高いということですので、AD は狭い一方で、AD 内であれば、トレーニングデータと同じ精度で予測できると考えられます。
アンダーフィッティングしているということは、AD が広いということです。アンダーフィッティングしており、トレーニングデータにおける予測精度は低いため、AD が広いとはいえその程度の精度になってしまいます。
このようにオーバーフィッティングやアンダーフィッティングを AD の広さと考えることで、AD により定量的な議論ができるようになります。
サンプル数が増えれば AD が広がります。

モデルが “トレーニングデータのノイズ” に適合していたとしても (もちろん適合していなくても)、トレーニングデータと同じ精度で予測できる範囲が広がるわけです。これが、サンプル数を増やすことでモデルの予測精度が向上する理由の一つであり、AD によりサンプル数の増加によるモデルの予測精度の向上に関する議論が定量的にできます。
なお、トレーニングデータとテストデータを分けるとき、基本的にランダムに分けると思います。これはトレーニングデータとテストデータのサンプル分布がなるべく同じになるように、というねらいがあります。サンプル分布が同じと仮定できれば、AD を明示的に設定することなく、ある妥当な AD 内での予測精度を議論することができるわけです。ただ、テストデータにおける予測精度が低いときに、アンダーフィッティングしているのか、オーバーフィッティングしているのか、オーバーフィッティングしているのであれば本当に使えないモデルなのかは、トレーニングデータにおける予測精度や AD を確認する必要があります。
線形の重回帰分析における共線性・多重共線性の問題も、AD で考えるとよいです。説明変数の間の相関が強いとき、回帰係数の値が正に大きくなる説明変数や、負に大きくなる説明変数が出てくることがあります。目的変数と説明変数の間に想定される関係を考えたとき、おかしな値であることが多いですが、回帰係数の値が大きくなること自体は問題ではありません。少なくともトレーニングデータには合っているわけで、トレーニングデータと同じようなサンプルであれば問題なく予測できます。問題なのは、AD が狭くなってしまうことです。トレーニングデータのサンプルの領域から、少しでも外れてしまうと目的変数の誤差が大きくなってしまうわけです。回帰係数を求めること自体が目的であれば話は別ですが、そうでない限りは、回帰係数の妥当性でモデルを評価するのではなく、トレーニングデータにおける予測精度と AD でモデルを評価するとよいです。
オーバーフィッティングやアンダーフィッティングの問題を AD の広さで考えることで、トレーニングデータにおける予測精度と AD といった2軸で定量的にモデルを評価できるようになります。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


