金子研の論文が Chemometrics and Intelligent Laboratory Systems に掲載されましたので、ご紹介します。タイトルは
Extended Gaussian Mixture Regression for Forward and Inverse Analysis
です。
目的変数 Y (複数でも OK) の値から説明変数 X の値を直接予測する直接的モデル解析法として Gaussian Mixture Regression (GMR) があります。
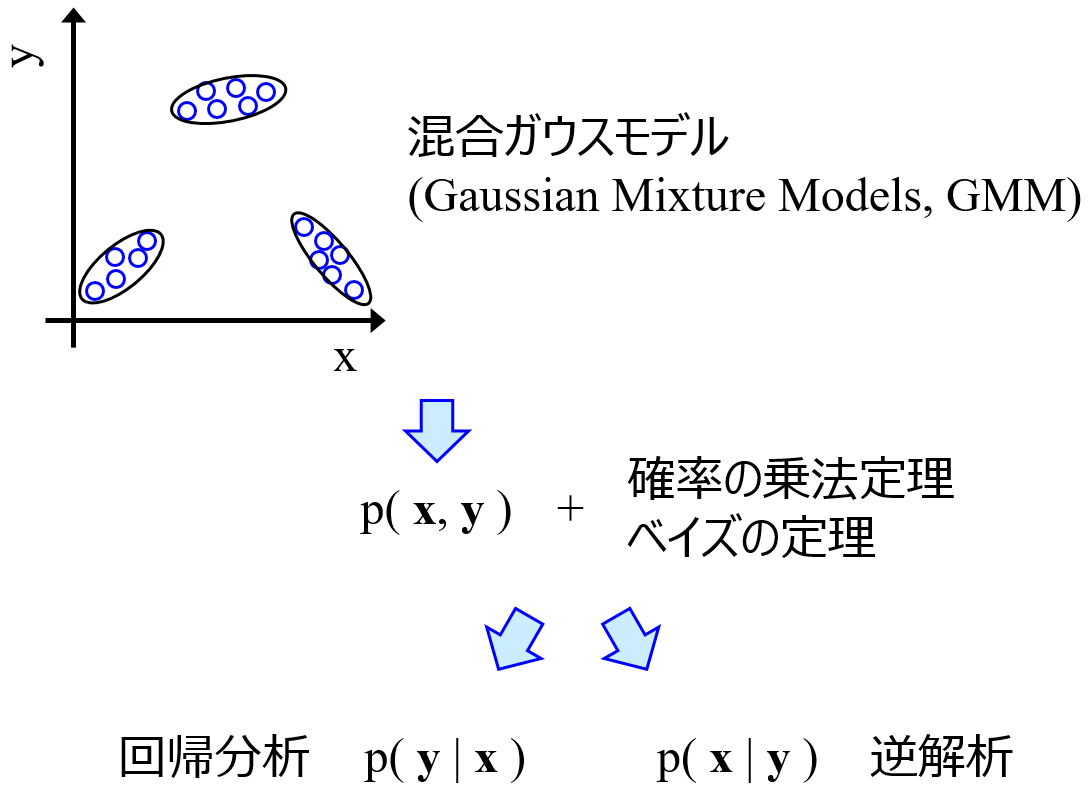


X と Y の間の関係を混合正規分布で表現することで、確率の乗法定理とベイズの定理より、Y の値が与えられたときの X の事後分布を計算できます。そして事後分布における X の確率が高い値が予測されます。GMR は、複数の Y をもつ材料設計に応用されたり、適応的実験計画法においてベイズ最適化を上回る性能をもつことが確認されたりしました。
GMR における Gaussian Mixture Models のパラメータを推定する方法として、EM アルゴリズムが一般的ですが、変分ベイズ法を用いることで、各パラメータに事前分布を設定して安定的にパラメータを推定できます。
GMR により X から Y を予測する場合でも Y から X を予測する場合でも、GMR の予測性能が重要なことから、本論文では GMR の予測精度を向上することを目的として、Extended GMR (EGMR) を開発しました。EGMR は、EM アルゴリズムによりパラメータ推定をする GMR と変分ベイズ法によりパラメータ推定をする GMR (Bayesian GMR, BGMR) を含みます。GMR には正規分布の数、正規分布における分散共分散行列の種類といったハイパーパラメータがあり、BGMR では正規分布の数、正規分布における分散共分散行列の種類、事前分布の種類、事前分布のパラメータといったハイパーパラメータがあります。さらに、GMR と BGMR のどちらも、確率密度分布からの予測値の計算方法を決める必要があります。EM アルゴリズムと変分ベイズ法のどちらを用いるかもハイパーパラメータとしてとらえ、クロスバリデーションで最も予測精度の高いハイパーパラメータを選択し、最終的な GMR モデルを構築します。
数値シミュレーションデータを用いて GMR と EGMR の順解析および逆解析を検証したところ、どちらも GMR より EGMR のほうが、予測精度が高いことを確認しました。さらに、分子設計、材料設計、スペクトル解析のデータセットを用いて GMR に対する EGMR の優位性を検証しました。
興味のある方は、ぜひ論文をご覧いただければと思います。ご検討のほどよろしくお願いいたします。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。