金子研の論文が Journal of Chemometrics に掲載されましたので、ご紹介します。タイトルは
Estimating the Reliability of Predictions in Locally Weighted Partial Least-Squares Modeling
です。
適応型ソフトセンサーの一つに Just-In-Time (JIT) 法によるソフトセンサーがあります。
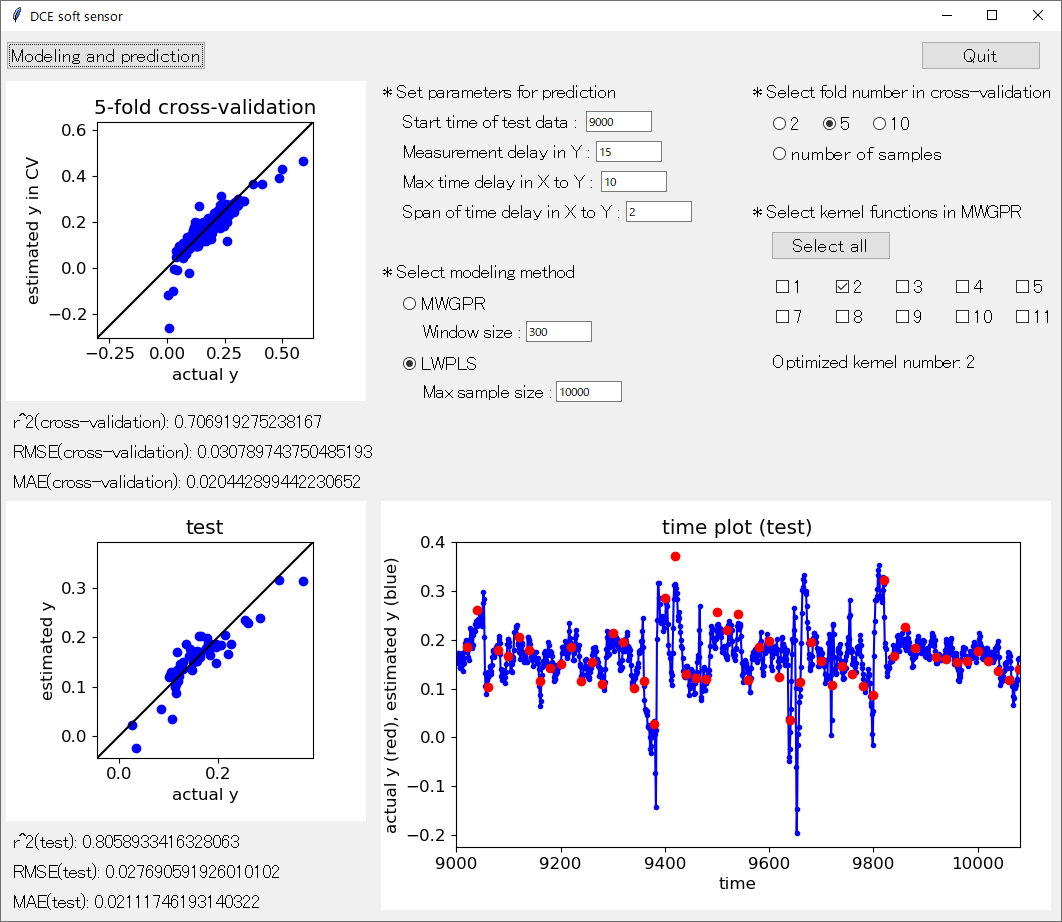

JIT 法の一つが、Locally-Weighted Partial Least Squares (LWPLS, 局所PLS) です。
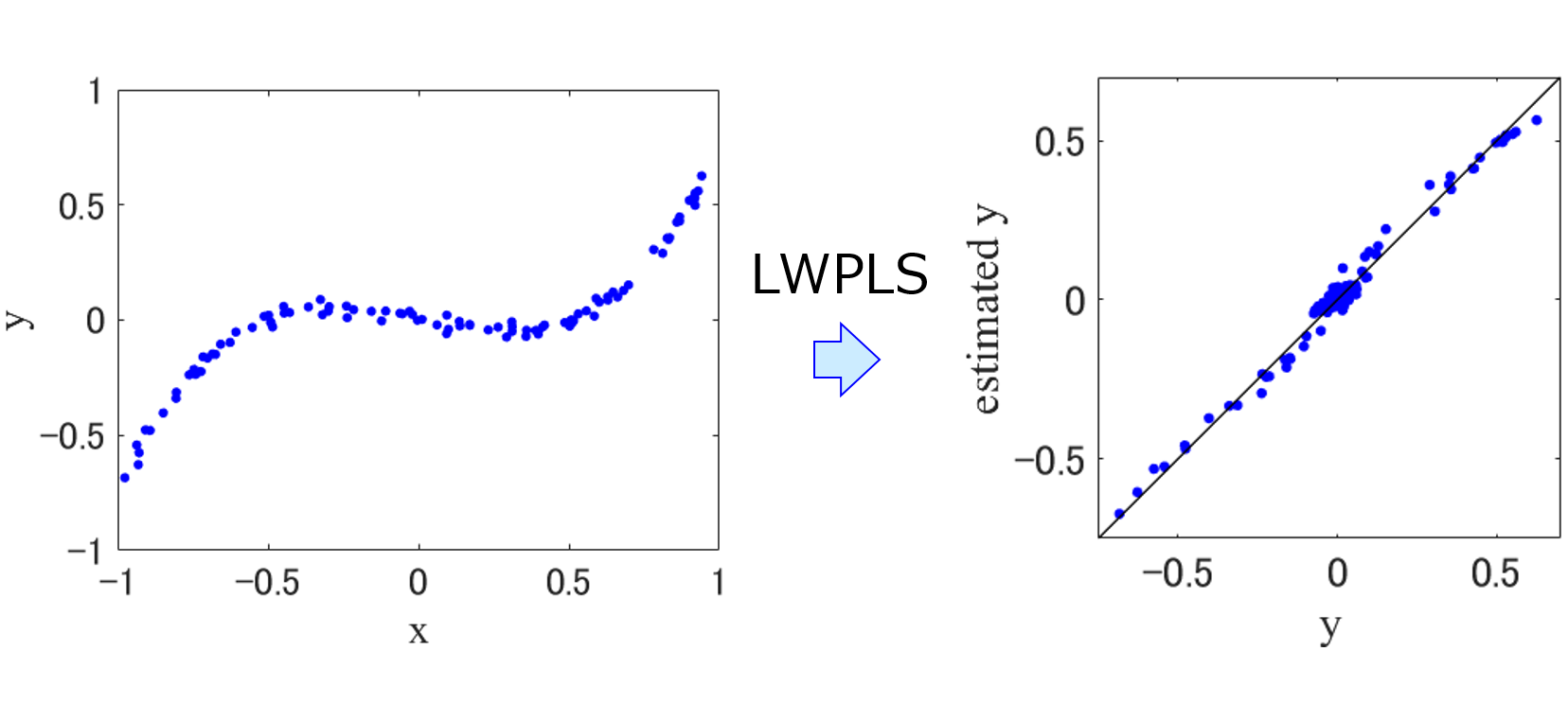
LWPLS は、特徴量間の共線性に強い部分的最小二乗回帰 (Partial Least Squares Regression, PLS) を、特徴量間の非線形性にも対応できるよう改良した手法です。LWPLS は、予測する説明変数 x のサンプルが与えられるごとに、回帰モデル自体が柔軟に変わります (予測するサンプルごとに別のモデルが構築されます)。 これにより装置やプラントにおけるプロセス状態が時々刻々と変化する場合においても、的確に目的変数 y の値を予測できため、私もよく LWPLS を使用しています。
ただ、LWPLS には欠点があり、その一つが y の予測誤差を推定する手法がないということでした。
そこで本研究では、モデルの適用範囲 (Applicability Domain, AD) の考え方を活用して、https://datachemeng.com/applicabilitydomain/
LWPLS における AD の指標を開発し、さらにその指標と予測誤差の関係を定量的にモデル化し、LWPLS モデルで y を予測するごとに、その予想誤差の標準偏差をエラーバーとして推定する手法を開発しました。
AD の指標は、予測する x のサンプルに対して、LWPLS モデルを構築するときのデータセットにおける、最も近いサンプルとの間の距離です。k 近傍法 (k-Nearest Neighbor, k-NN) おける 1-NN の距離に対応します。なぜこの指標にしたかというと、LWPLS は予測するサンプルとの間の距離が小さい (トレーニングデータの) サンプルほど、重みが大きくなるようにサンプルごとの重みを設定して PLS モデルを構築する手法であり、距離が小さいサンプルがあるほど的確に y を予測できると考えられるためです。
この指標である最小距離と、クロスバリデーションによって計算された y の誤差の標準偏差の間の関係を、線形関数・指数関数・シグモイド関数により仮定します。すべての関数でフィッティングを行い、最も精度よくフィッティングできた関数が、y の予測誤差推定モデルとして採用されます。この予測誤差推定モデルを LWPLS モデルと併用することで、y 値の予測をしながら、同時にその予測誤差の標準偏差も推定することができます。推定された予測誤差の標準偏差に基づいて、2σ や 3σ といったエラーバーを設定できます。
脱ブタン蒸留塔や硫黄回収装置のデータセットを使ってデータ解析したところ、これらのプラントや装置においては、シグモイド関数が予測誤差推定モデルとして採用されました。さらに、LWPLS により適切に y の予測と予測誤差の推定をできることを確認しました。
興味のある方は、ぜひ論文をご覧いただければと思います。どうぞよろしくお願いいたします。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。