金子研オンラインサロンにおいて、ガウス過程回帰において、予測値の分散が正しく評価されているのか、どのように検証したらよいか?、といった質問があり、回答しました。
ガウス過程回帰の予測値の分散は、モデルの適用範囲やベイズ最適化にも活用され、

気になる方も多いかと思いますので、ここでも共有します。
ガウス過程回帰における目的変数 y の予測値については、他の回帰分析手法と同様に、例えばテストデータにおける y の実測値 vs. 予測値プロットを見たり、r2, RMSE, MAE を確認したりすることで検証できますが、
予測値の分散は、他の回帰分析手法にはない、ガウス過程回帰で特有の出力結果であり、別に検証する必要があります。
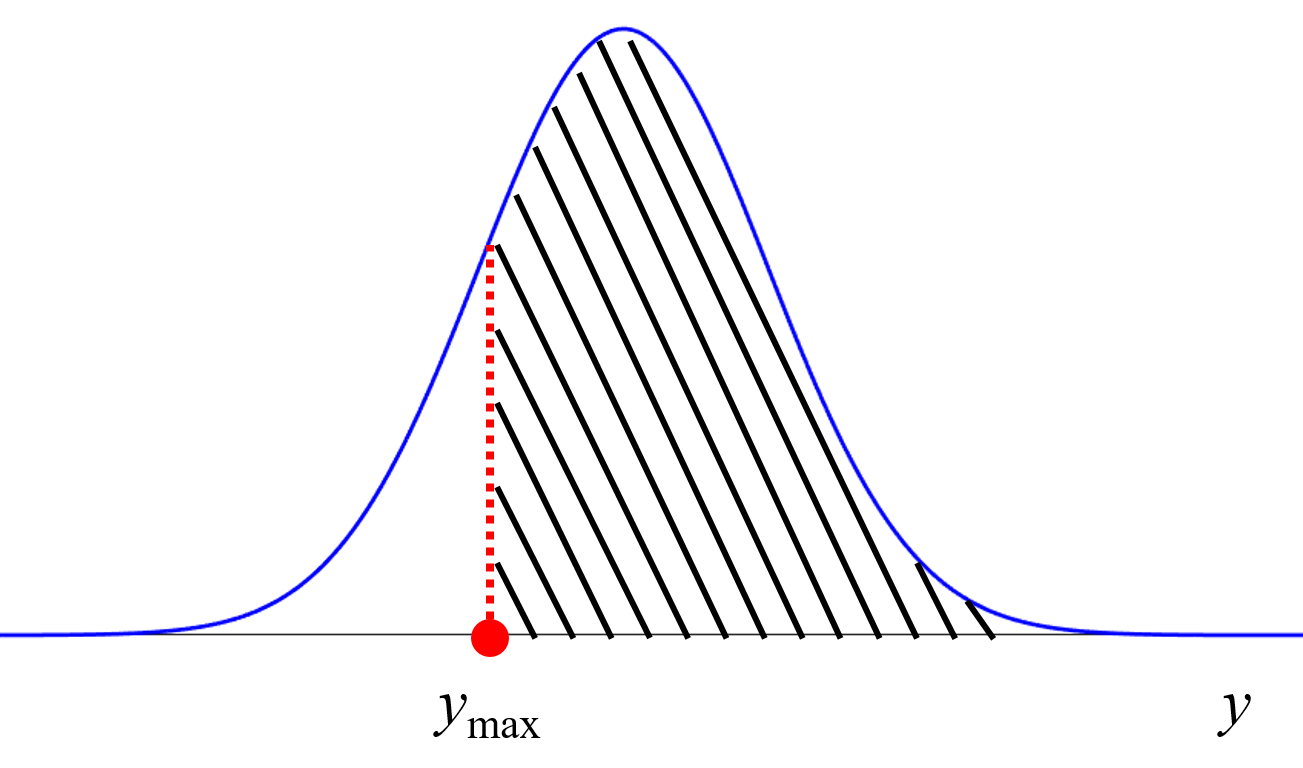
ガウス過程回帰では基本的に y が、予測値を平均値、予測値の分散 (ガウス過程回帰の出力結果) を分散とする正規分布に従うことを仮定しています。y の実測値と予測値の差 (予測誤差) については、平均値を y と仮定してよさそうですので、y の予測誤差が 0 を平均値、予測値の分散を分散とする正規分布に従うかどうかを検証します。例えばテストデータの y の実測値と予測値から予測誤差を計算しまして、それが、平均値が 0 で分散が y の予測値の分散となる正規分布に従えば、y の予測値の分散が正しく評価されている、といえます。
ただ、ガウス過程回帰における y の予測値の分散はサンプルごとに異なります。(テストデータの) サンプルを集めて、それが何らかの分布に従うかどうかを考えるときには、y の予測値の分散を正規化・標準化をする必要があります。そこで、サンプルごとに予測誤差を y の予測値の標準偏差 (y の予測値の分散の平方根) で割ることで、分散を 1 にそろえます。この標準化により、標準化後の予測誤差は平均値が 0、分散が 1 の正規分布に従うと仮定できます。例えばテストデータにおける標準化後の予測誤差が平均値 0、分散 1 の正規分布に従っていれば、ガウス過程回帰によって適切に y の予測値の分散を評価できているといえます。
ちなみに、平均値 0、分散 1 の正規分布に従うかは、ヒストグラムを確認したり、Q-Q (Quantile-Quantile) プロットを確認したり、正規性の検定をしたりします。正規性の検定としては、コルモゴロフ–スミルノフ検定やシャピロ–ウィルク検定やアンダーソン–ダーリング検定などがあります。SciPy にそれぞれ実装されています。
なおここでは例として、テストデータで検証することを想定して説明しましたが、サンプル数が小さい場合は、テストデータにおける予測誤差と予測値の分散の代わりに、ダブルクロスバリデーションにおける予測誤差と予測値の分散を用いるとよいです。

ガウス過程回帰における y の予測値の分散が適切に評価されているか検証したい場合は、以上の方法を用いるとよいと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。