説明変数 x と目的変数 y の間で回帰モデルやクラス分類モデルを構築するとき、いろいろな回帰分析手法やクラス分類手法があります。x のすべての特徴量が平等に重要な場合もあれば、x の中に重要な特徴量もあり重要でないノイズのような特徴量もある場合もあります。後者のとき、特徴量の重要度を考慮することで、より的確なモデルを構築できると考えられます。ただ回帰分析手法やクラス分類手法の中には、特徴量の重要度が考慮されていない手法があります。代表的な例としては、ガウシアンカーネルを使用したときのサポートベクターマシン (Support Vector Machine, SVM) やサポートベクター回帰 (Support Vector Regression, SVR) です。
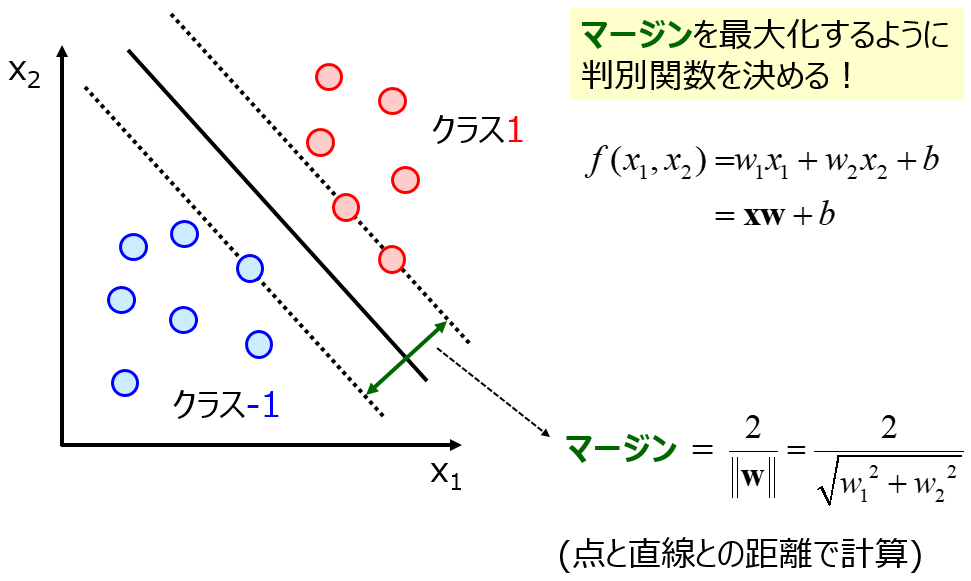

ガウシアンカーネルを使用した SVM も SVR も非線形の手法ですが、サンプル間のユークリッド距離に基づくため、特徴量の重要度は考慮されていません。ガウス過程回帰 (Gaussian Process Regression, GPR) も、使用するカーネル関数の種類によっては特徴量の重要度を考慮できません (例えばガウシアンカーネル)。

ただ、経験された方もいらっしゃると思いますが、ガウシアンカーネルを使用した時の SVM や SVR や GPR の結果が、他の特徴量の重要度を考慮した手法より良好になることも多くあります。特徴量の重要度を考慮しない手法でも、予測的なモデルを構築することができます。
そもそも、特徴量の重要度とはいえ、それが特徴量の真の重要性を表しているとは限りません。今あるデータセットに合うように特徴量の重要度が割り当てられるため、オーバーフィッティングをしている可能性も考えられます。特に、サンプル数が小さいときにはオーバーフィッティングしやすい状況にあり、偶然の相関によって特徴量の重要度が割り当てられる可能性も高いです。このような状況のとき、各特徴量を平等に扱うことで、オーバーフィッティングを低減しているともいえます。
特徴量の重要度を考慮したほうがよいかどうかはデータセットによって異なります。そのため特徴量の重要度を考慮できる手法だけでなく考慮できない手法も含めて、モデル構築やモデルの予測精度の評価を検討するとよいでしょう。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


