タイトルを見て、線形モデルは回帰係数 (各特徴量の目的変数に対する重み) が与えられるのだから、線形モデルを解釈できるのは当たり前では??、と考えた方、非常に危険です。以下、必見です。
金子研の論文が ACS Omega に掲載されましたので、ご紹介します。タイトルは
Genetic Algorithm-Based Partial Least-Squares with Only the First Component for Model Interpretation
です。
分子設計、材料設計、プロセス設計、プロセス管理・制御において、説明変数 x と目的変数 y の間で予測精度の高いモデルを構築することだけでなく、現象を説明したりメカニズムを解明したりするため構築されたモデルを解釈することも重要です。
例えばランダムフォレストの feature importance により、y を予測する上での x の重要度を計算できます。SHAP や LIME では、あるサンプル点におけるモデルの近似式を求めることで、そのサンプル点回りにおける y に対する x の傾きを求められます。
x と y の間の関係が線形のときは、線形のモデリング手法を用いることで予測精度の高いモデルを構築できます。さらに、線形モデルでは、y に対する x の重み、すなわち回帰係数が与えられます。しかし、回帰係数を y に対する x の寄与度とすることは非常に危険です。なぜなら x の間には多重共線性があるためです。ある二つの x 同士に相関関係があるとき、一つの x の回帰係数を正に大きく、もう一方の x の回帰係数を負に大きくすることで、バランスを保とうとします。詳細はこちらをご覧ください。

そこにも書かれている通り、回帰係数の値を y に対する x の寄与度とできるのは、x の間に多重共線性がまったくないときか、x がたった 1 つのときのみです。前者は現実的でないことから、ここでは x が 1 変数で回帰することに着目し、PLS の 1 成分モデルを採用します。
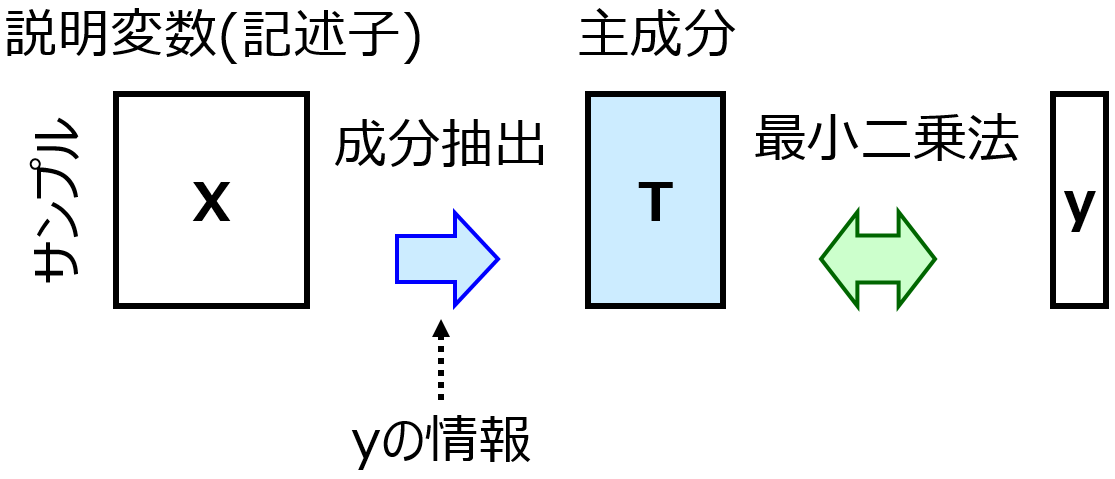
PLS の主成分が一つだけであるため、主成分の回帰係数を x に対する主成分の寄与度とすることができます。そのため、その主成分の回帰係数とローディングやウェイトを用いて計算される、x の回帰係数を、y に対する x の寄与度とすることができます。この手法を PLS with only the First Component (PLSFC) と呼びます。PLSFC による回帰係数により y に対する x の寄与度を解釈します。
しかし PLSFC では、特に x の数が大きいときに、1 成分のみでは予測精度の高いモデルを構築することが困難です。予測精度の低いモデルをいくら解釈しても意味がありません。そこで PLSFC と遺伝的アルゴリズム (Genetic Algorithm, GA) を組み合わせて、PLS の 1 成分モデルの予測精度が高くなるように、x の選択をする手法を提案します。GA の適合度を、1 成分 PLS モデルのクロスバリデーションによる予測精度とすることで、予測精度の高い x の組み合わせと、その x の解釈可能な重みを獲得できます。なお、GA はオーバーフィッティングの危険が高いですが、今回は 1 成分モデルであるため、例えば PLS の成分数をクロスバリデーションで最適化する場合と比較して、オーバーフィッティングの危険は小さくなる、というメリットもあります。この手法を GA-based PLSFC (GA-PLSFC) と呼びます。
GA と PLS に基づく特徴量選択として、スペクトル解析では波長や波数の方向に幅を持って特徴量を選択する GAWLS-PLS、プロセスデータではプロセスの動特性もしくはプロセス変数の y に対する時間遅れを考慮しながら特徴量を選択する GAVDS-PLS に着目します。
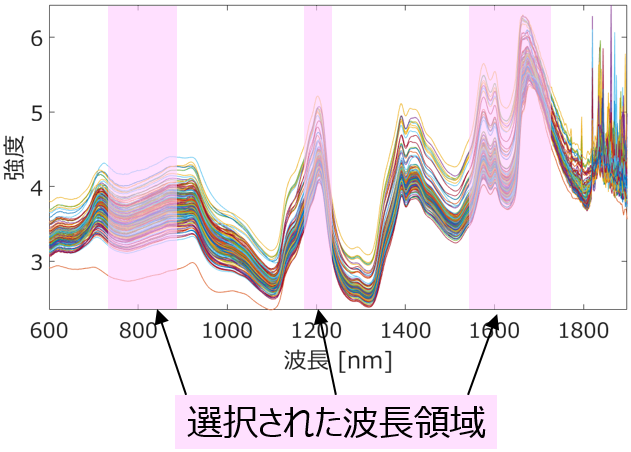
それぞれにおいて PLSFC を用いた特徴量選択手法を GAWLS-PLSFC, GAVDS-PLSFC と呼びます。
論文では、数値シミュレーションデータセット、分子や材料のデータセット、スペクトルのデータセット、プロセスの時系列データセットを用いて提案手法 GA-PLSFC, GAWLS-PLSFC, GAVDS-PLSFC の予測精度や解釈性を検証しました。その結果、提案手法により予測精度が高く、かつ解釈性の高いモデルを構築できることを確認しました。
興味のある方は、ぜひ論文をご覧いただければと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


