分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・実験条件・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と分子・材料の物性・活性・特性や製品の品質などの目的変数 y との間で数理モデル y = f(x) を構築し、構築したモデルに x の値を入力して y の値を予測したり、y が目標値となる x の値を設計したりします。
データセットの可視化・見える化や外れ値検出などを目的として、x を 2 次元に低次元化し、平面上でサンプルを確認します。

手法としては、主成分分析(PCA)や GTM、t-SNE などがあります。

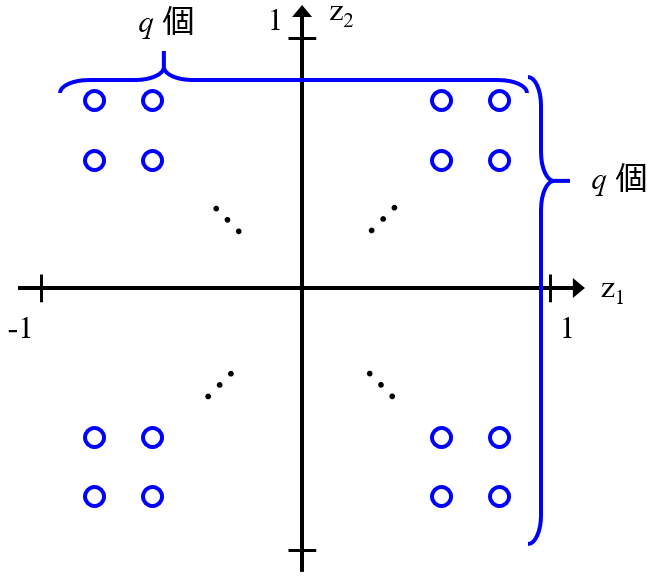
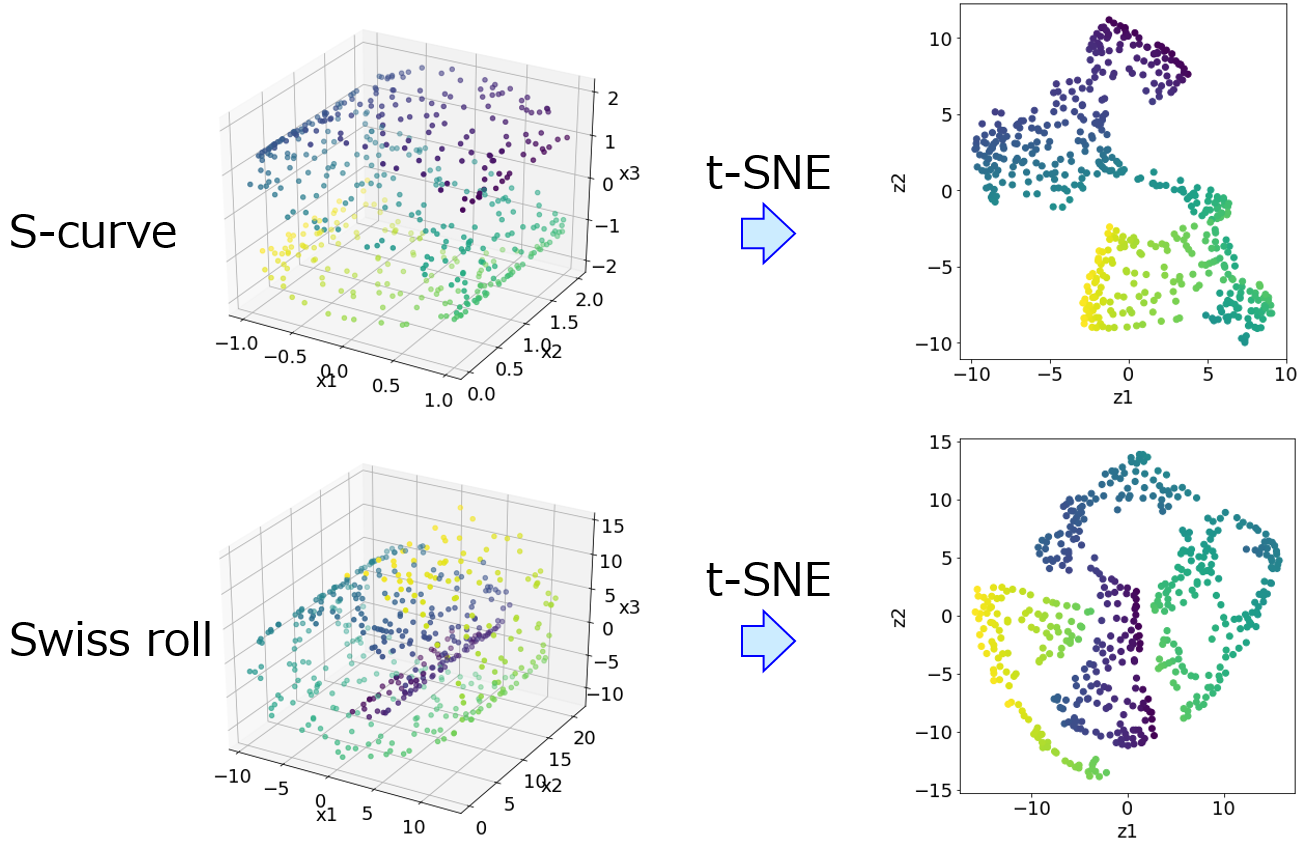
手法ごとの可視化性能の評価や手法の選び方については、こちらが参考になります。

学会発表や論文などで、2 次元平面を示してサンプル同士が近いとか遠いとか議論することもありますし、そうした議論を目にすることもあると思います。2 次元平面上でサンプルが近いと、「似ているサンプルなんだなあ」と思わせてしまう何かが確かにあります。しかし、実際の x におけるサンプル間の距離と、2 次元平面上での距離は一致しないため、注意が必要です。2 次元平面上では近くにあるサンプルでも、実際の x では似ていないことがありますし、逆に、x では似ているにもかかわらず、2 次元平面上では離れて見えることも起こります。
2 次元平面上でサンプル間の距離もしくは類似度を議論するためには、どの程度の情報量が可視化されているかを確認した方が良いです。例えば主成分分析では、累積寄与率を計算することで、多次元上の x のデータセットのうち何パーセントが 2 次元平面上に表現されているかを確認できますが、他の非線形の可視化手法では、2 次元平面上で表現された情報量を確認することはできません。もちろん、非線形であるため、主成分分析より 2 次元平面上の情報量は多いと考えられますが、具体的な数値は示されません。その意味で、どんな可視化手法を用いる場合でも、少なくとも主成分分析における累積寄与率は確認しておいた方が良いと考えています。例えば、累積寄与率が 60% である場合、他の非線形手法を用いた可視化の結果においても、60% 以上表現されている可能性が高い、といったように考えられます。
x の変数を変えながら可視化をして、自分がもともと持っている結論に近い結果が出た場合にのみ、それを採用する、ということをしてしまうと、客観的にデータセットを可視化しているのではなく、ただ「見たいものを見ているだけ」になってしまいます。注意が必要です。
では、x をそのまま用いて、x の空間におけるサンプル同士の近接関係を可視化する方法は?、というと、クラスタリングが挙げられます。クラスタリングにおいては、サンプル間の距離もしくは類似度の計算に x そのものを使用しますので、クラスタリングの結果において似ているとされたサンプルは、実際の x でも似ています。同じクラスターにあるサンプル同士は似ていますし、また階層的クラスタリングのデンドログラムを見ることで、どのクラスター同士が似ているかも確認できます。
もちろん、2次元平面上における可視化・見える化は、データセットの解釈や議論がしやすくなるという点で非常に有効な手段の一つです。ただし、実際の x におけるサンプル同士の近接関係と、2 次元平面上でのサンプル同士の近接関係が異なることが多いため、どんな可視化手法を用いるにしても、主成分分析における累積寄与率を確認したり、クラスタリングを併用して2 次元平面上で似ているサンプル同士が同じクラスターに属しているかを確認したりすると良いでしょう。
以上です。
質問やコメントなどありましたら、X, facebook, メールなどでご連絡いただけるとうれしいです。


