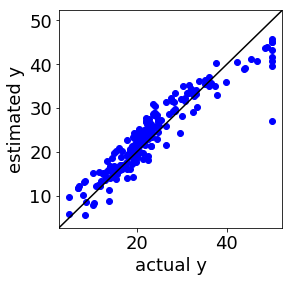
SVR (Support Vector Regression, サポートベクター回帰) で回帰モデルを構築したことのある方は、下の図のように、実測値 vs. 推定値プロットにおいて、対角線から一定に離れたところにサンプルが固まっている、つまり全く同じ誤差のサンプルがある、ことを経験しているのではないでしょうか。

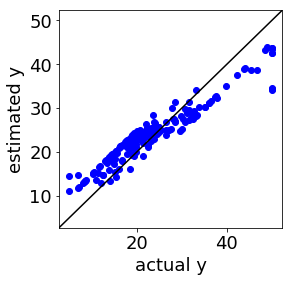
補助線を入れるとこんな感じでしょうか。赤い点線のところに、つまり ε チューブの境界に、サンプルが固まっています。

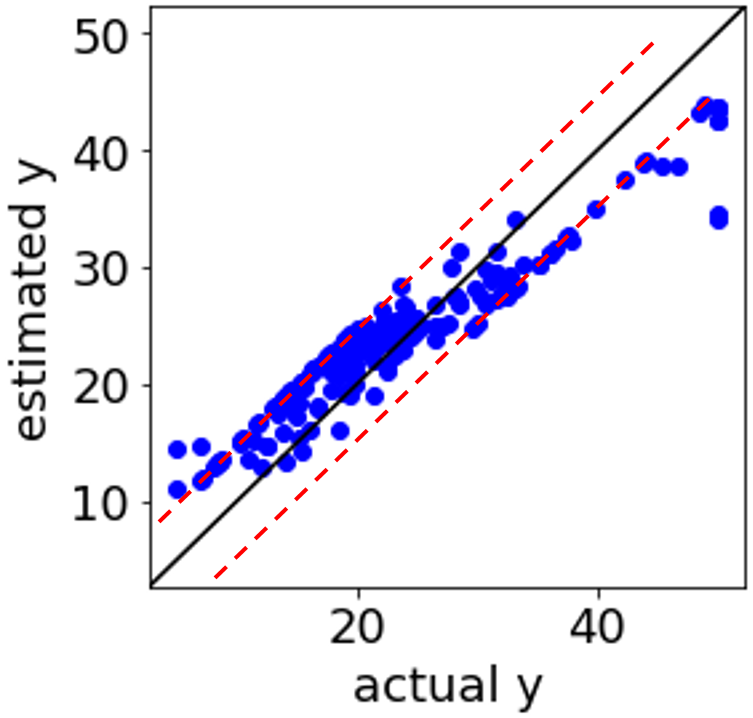
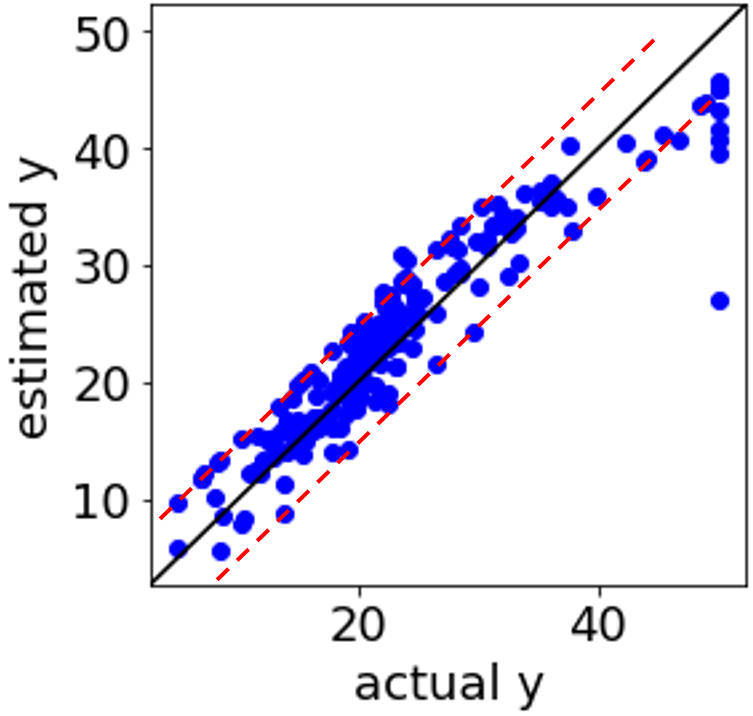
違和感のある実測値 vs. 推定値プロットですので、何か解析方法に問題があるのかと疑ってしまう方もいらっしゃるのではないでしょうか。実はこの現象自体にはまったく問題はありません。

今回は全く同じ誤差のサンプルがある理由を解説します。

SVR に関して、まずこちらをご覧ください。

サポートベクター回帰(Support Vector Regression, SVR)～サンプル数10000以下ならこれを使うべし！～

サポートベクター回帰(Support Vector Regression, SVR)について、pdfとパワーポイントの資料を作成しました。データセットが与えられたときに、SVRで何ができるか、SVRの特徴、どのように計算するかが説明されてい...

SVR の式は

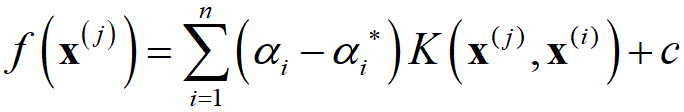
でして、α_i, α_i* は

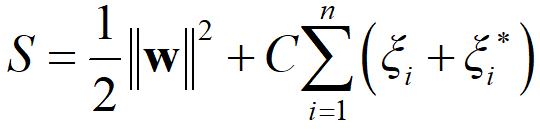
を最小にするようにして、ラグランジュの未定乗数法で最適化されます (他の記号については SVR の解説をご覧ください)。なお、0 ≤ α_i, α_i* ≤ C です。

α_i, α_i* の最適化の過程において、ラグランジュ乗数とそれと対応する制約式の積が0 となる条件である、カルーシュ・クーン・タッカー条件 (Karush-Kuhn-Tucker condition, KKT条件) が、以下の式で与えられます。

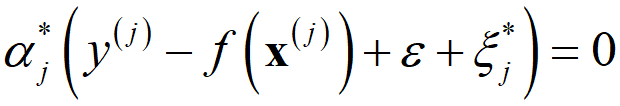
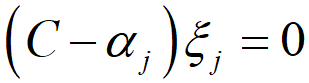
1 つ目の式より、α_j が 0 以外の値となるのは、(f(x^(j)) + ε + ξ_j − y^(j)) = 0 つまり y^(j) = f(x^(j)) + ε + ξ_j となるサンプルのみであり、それらは ε チューブの上側の境界にあるサンプル (ξ_j = 0) か ε チューブの上側の外にあるサンプル (ξ_j > 0) です。2 つ目の式より α_j* が 0 以外の値となるのは、(y^(j) − f(x^(j)) + ε + ξ_j*) = 0 つまり y^(j) = f(x^(j)) − ε − ξ_j* となるサンプルのみであり、それらはε チューブの下側の境界にあるサンプル (ξ_j* = 0) か ε チューブの下側の外にあるサンプル (ξ_j* > 0) です。

さらに (f(x^(j)) + ε + ξ_j − y^(j)) = 0 と (y^(j) − f(x^(j)) + ε + ξ_j*) = 0 に着目して両辺の和を取ると、2ε + ξ_j + ξ_j* = 0 となり、ε > 0, ξ_j ≥ 0, ξ_j* ≥ 0 からこの式は成り立ちません。よって (f(x^(j)) + ε + ξ_j − y^(j)) = 0 と (y^(j) − f(x^(j)) + ε + ξ_j*) = 0 が同時に成り立つことはないわけです。このことから、すべてのサンプル (y^(j), x^(j)) において、少なくとも α_j = 0 もしくは α_j* = 0 となります。

よって、1 つ目の式・2 つ目の式の話と組み合わせると、ε チューブの内側にあるサンプルでは、α_j = α_j* = 0 となります。このようなサンプルは、一番最初の SVR モデルの式にまったく寄与しません。それ以外のサンプル、つまり ε チューブ上のサンプルもしくはε チューブの外側のサンプルのことをサポートベクターと呼び、SVR モデルの式はサポートベクターのみによって決まります。

0 < α_j < C となるサンプル (y⁽ⁱ⁾, x⁽ⁱ⁾) は、4 つの式の 3 つ目より ξ_j = 0 です。よって y⁽ⁱ⁾ = f(x⁽ⁱ⁾) + ε です。これらのサンプルは、誤差がちょうど ε ということです。また、0 < α_j* < C を満たすサンプル (y⁽ⁱ⁾, x⁽ⁱ⁾) は、4 つの式の 4 つ目より ξ_j* = 0 です。よって y⁽ⁱ⁾ = f(x⁽ⁱ⁾) − ε です。これらのサンプルは、誤差がちょうど −ε ということです。

つまり、上の図の赤い点線上に固まっているサンプルは、モデル構築における最適化の段階で、0 < α_j < C や 0 < α_j* < C となったサンプルであり、特に問題はありません。

最後に α_j, α_j* の値ごとのサンプルの説明を下にまとめます。

α_j = 0, α_j* = 0 : ε チューブの内側のサンプル。SVR モデルの式に寄与しない
0 < α_j < C, α_j* = 0 : 上側の ε チューブ上のサンプル。サポートベクター。定数項の計算に使用
α_j = 0, 0 < α_j* < C : 下側の ε チューブ上のサンプル。サポートベクター。定数項の計算に使用
α_j = C, α_j* = 0 : ε チューブの上側のサンプル。サポートベクター
α_j = 0, α_j* = C : ε チューブの下側のサンプル。サポートベクター

よって、SVR の特徴として

ε チューブの内側のサンプル、つまり誤差が小さいサンプルは、SVR モデルに影響しないため、SVR モデルはノイズの影響を受けにくい
ε チューブの上側のサンプルやε チューブの下側のサンプル、つまり誤差が大きいサンプルは、どんなに誤差が大きくても、SVR モデルへの影響を C でコントロールできるため、SVR モデルは目的変数の外れ値の影響は受けにくい

があります。