回帰モデルやクラス分類モデルを評価するときの話です。評価のときに、クロスバリデーションやダブルクロスバリデーションが使われることもありますが、


それぞれ何のために、何を評価しているのか?についてお話します。
そもそも、どうしてモデルを評価したいかというと、複数のモデルがあるときにどれを使えばよいのか決めたいからです。たとえば回帰分析して、部分的最小二乗法 (Partial Least Squares, PLS) とサポートベクター回帰 (Support Vector Regression, SVR) でそれぞれ回帰モデルを構築したとします。
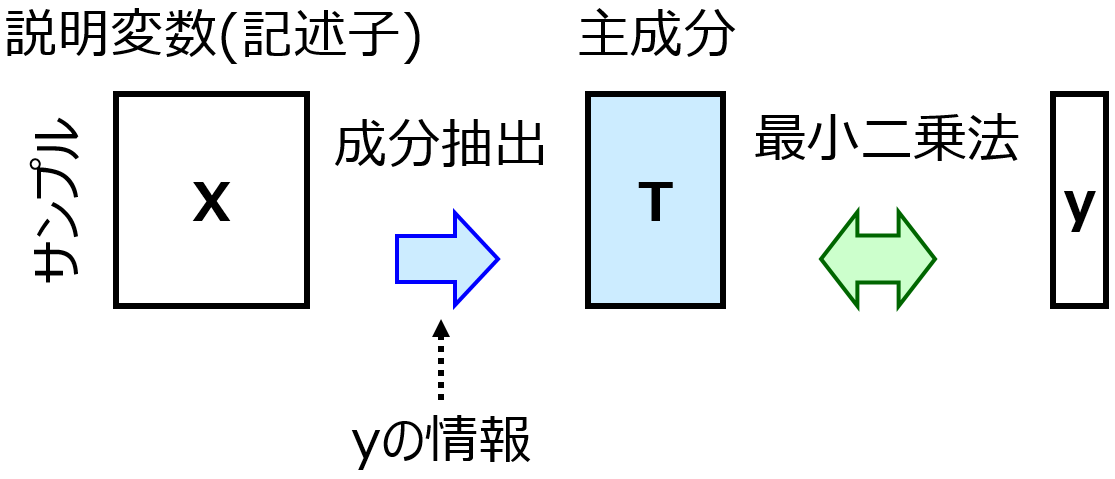

このとき、PLS モデルと SVR モデルとで、どちらのほうがよいのかを決めるため、2つのモデルを評価・比較します。
たとえば 1000 サンプルあるときに、1000 サンプルで PLS モデルと SVR モデルを構築して、同じ 1000 サンプルを推定した結果を評価に使ってはどうでしょうか。これはよくありません。PLS モデルや SVR モデルでやりたいことは、1000 サンプルにおける説明変数 (記述子・特徴量・入力変数) X と目的変数 Y との間の関係を説明することではありません。新しいサンプルの X の値をモデルに入力して、y の値を精度よく推定することです。1000 サンプルで構築したモデルの推定性能を、同じ 1000 サンプルで評価すると、新しいサンプルに対する推定性能を評価できません。
なので、まず 1000 サンプルを 2 つに分けます。たとえば 700 サンプルと 300 サンプルといった感じです (あわせて 1000 サンプルです)。700 サンプルで PLS モデルと SVR モデルを構築して、300 サンプルの推定結果を 2 つのモデルの評価に使おう、というわけです。PLS モデルのほうが SVR モデルより 300 サンプルを精度よく推定できたら、SVR モデルではなく PLS モデルを使おう!となります。
一点、注意することは、最終的に用いる PLS モデルは、700 サンプルで構築された PLS モデルではなく、すべてのサンプルである 1000 サンプルで構築された PLS モデルです。本当は、1000 サンプルで構築された PLS モデルと SVR モデルの新しいサンプルに対する推定性能を評価したいのです。しかしそれは難しいので、700 サンプルで構築された PLS モデルと SVR モデルの新しいサンプルに対する推定性能の優劣は、1000 サンプルで構築された PLS モデルと SVR モデルの新しいサンプルに対する推定性能の優劣と等しいと仮定して、評価しているわけです。
そのため、700 サンプルで構築されたモデルと 1000 サンプルで構築されたモデルとは似ている必要がありますので、700 サンプルと 1000 サンプルも似ていなければなりません。実際、1000 サンプルから 700 サンプルを選んでおり、実は 700 サンプルといわず、なるべく多くの (1000 に近い数の) サンプルを使いたいのが正直なところです。ただ、このサンプル数を大きくしてしまうと、構築したモデルを評価するようのサンプル (さきほどの 300 サンプル) が少なくなってしまい、評価結果の信憑性がなくなってしまいます。このあたりがジレンマなのです。
ジレンマは仕方ないとしても、1000 サンプルをたとえば 700 サンプルと 300 サンプルとにあらかじめ分けておくことで、PLS モデルと SVR モデルのどちらを用いるか決められます。
ただし、PLS モデルといっても、実は一つではありません。主成分を何成分まで用いるかで PLS モデルは変わります。SVR モデルについても、C, ε, γ (ガウシアンカーネルを用いる場合) としてどの値を用いるかで SVR モデルは変わります。詳しくは PLS や SVR の説明をご覧ください。


このような主成分の数, C, ε, γ のようなパラメータのことをハイパーパラメータといいます。
では、ハイパーパラメータの値の異なる、複数の PLS モデル・複数の SVR モデルがあるなかで、すべて 700 サンプルでモデルを構築して、300 サンプルの推定を行い、推定結果が最もよいモデルをそれらの中から選んで、そのモデル (たとえば成分数が 3 の PLS モデル) を最終的なモデルとして使うことにしましょうか?
実はこれはよくありません。300 サンプルの推定結果について、少数のモデルの推定性能を比較するのには使ってよいですが、たくさんのモデルの中から最良なものを選ぶような最適化には使えません。この理由は先ほどのジレンマと関係します。300 サンプルはただただ 1000 サンプルから選んだサンプルです。700 サンプルで構築されたモデルにおいて、300 サンプルの推定結果がよければ、1000 サンプルで構築したモデルの新しいサンプルに対する推定結果もよい、と仮定しているだけなのです。300 サンプルの推定結果がよいモデルを多数のモデルの中から選んで最適化してしまうと、その 300 サンプルだけに特化したモデルになってしまいます。300 サンプルにオーバーフィットしてしまうわけです。
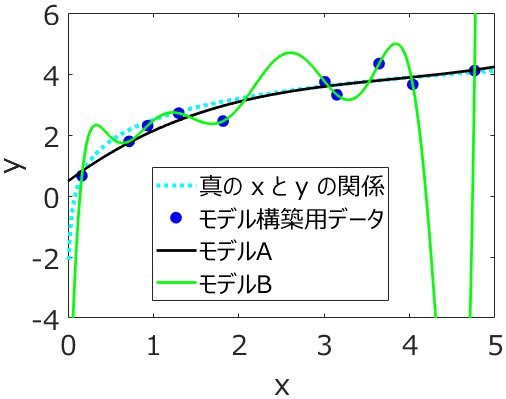
なので、300 サンプルの推定結果を比較するときまでに、少数のモデルに絞っておく必要があるのです。ただ、いくつが “少数” なのかは不明です。実際は、PLS モデルで一つ、SVR モデルで一つ、といった具合に、手法ごとに一つのモデル、つまり一つのハイパーパラメータの値、を事前に選んでおくのが一般的です。
このPLSやSVRといった一つの手法の中における、事前のモデルの絞り込み、言い換えるとハイパーパラメータの選択、には、700 サンプルでクロスバリデーションをすることが一般的です。

クロスバリデーションで、PLS, SVR などの一つの手法があるときに、ハイパーパラメータの値を変えてそれぞれモデルの推定性能を評価し、それが最も高いハイパーパラメータの値を選びます。もちろん、クロスバリデーションといっても一つのバリデーションですので、先ほどの 700 サンプルと 300 サンプルに分けて推定性能を評価するとき話 (ジレンマやオーバーフィッティング) はそのまま当てはまります。たとえばクロスバリデーションで fold 数を決めるときには、ジレンマを考える必要があります。
もちろん、クロスバリデーションを使わずに、700 サンプルをさらに 500 サンプルと 200 サンプルといった具合に分け、200 サンプルの推定性能が高いハイパーパラメータの値を選ぶ、といったこともできます。ただ、そうするとさらにモデル構築用のサンプル数が小さくなってしまいますし、その 200 サンプルのみに特化したハイパーパラメータが選ばれてしまう恐れもあります。そのため、クロスバリデーションが使われます。
1000 サンプルがあるとき、まず 700 サンプルと 300 サンプルとに分けます。そして 700 サンプルでクロスバリデーションして一つの PLS モデル、一つの SVR を選びます。最後に、300 サンプルの推定結果を 2 つのモデル (PLS モデル・SVR モデル) で比較して、どちらのモデルを用いるか決めます。
上の、” 700 サンプルと 300 サンプルとに分ける” ところにもクロスバリデーションを使おう、というのがダブルクロスバリデーションです。

クロスバリデーションではある手法における、ハイパーパラメータの値ごとのモデルの推定性能を評価し、ダブルクロスバリデーションでは複数の手法間でのモデルの推定性能を評価します。ダブルクロスバリデーションを使うときでも使わないときでも、最終的なモデル (PLS モデルか SVR モデル) は、すべてのサンプル (1000 サンプル) で構築します。ダブルクロスバリデーションでも、700 サンプルと 300 サンプルに分けて推定性能を評価するとき話 (ジレンマやオーバーフィッティング) はそのまま当てはまりますので、注意が必要です。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。