回帰モデルでもクラス分類モデルでも、モデルを構築したらそのモデルの解釈をしたくなるものです。どの説明変数 (特徴量・記述子・パラメータ) が重要なのか、説明変数が目的変数にどのように寄与しているのか、などなどです。
たとえば説明変数の重要度でしたら、ランダムフォレストなどの 「決定木 + アンサンブル学習」 で検討することが可能です。
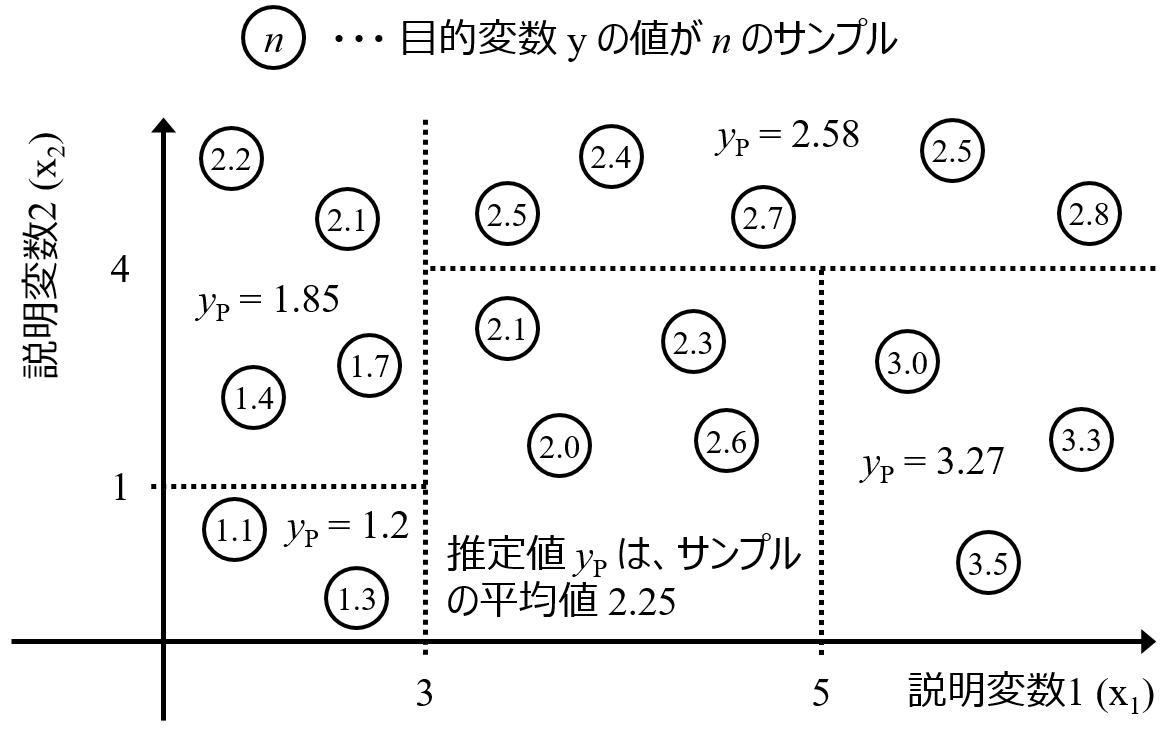

重要度の閾値 (重要度がいくつ以上なら重要か) については、Boruta でやっているような乱数で生成したデータセットを使えば、検討できます。

ただし、それぞれの説明変数が目的変数に対して正に効いているのか、負に効いているのかはわかりません。
線形の回帰モデルであれば、(標準)回帰係数を求めることができます。(標準化された) 説明変数の値に標準回帰係数の値をかけて足せば、目的変数の値になります。しかし、標準回帰係数を各説明変数の目的変数に対する寄与と考えるのは危険です。データセットにおいて説明変数の間には共線性・多重共線性がありますので、説明変数と目的変数との間の真の関係にかかわらず、説明変数間の関係も影響する形で、基本的に目的変数の誤差が小さくなるように標準回帰係数が決められます。
また、モデルが非線形ですと、そもそも標準回帰係数を求めることができません。ただ、やはりモデルがあるとその解釈をしたくなるもので、非線形モデルにおける説明変数の目的変数に対する寄与を計算するための指標が開発されてきました。たとえば、LIME (Local Interpretable Model-agnostic Explanations) [Github], SHAP (SHapley Additive exPlanations) [Github], DeepLIFT (Deep Learning Important FeaTures) [Github], Influence Functions [Github] などです。非線形モデルが微分可能であれば、各説明変数の微分係数もその指標の一つですね。
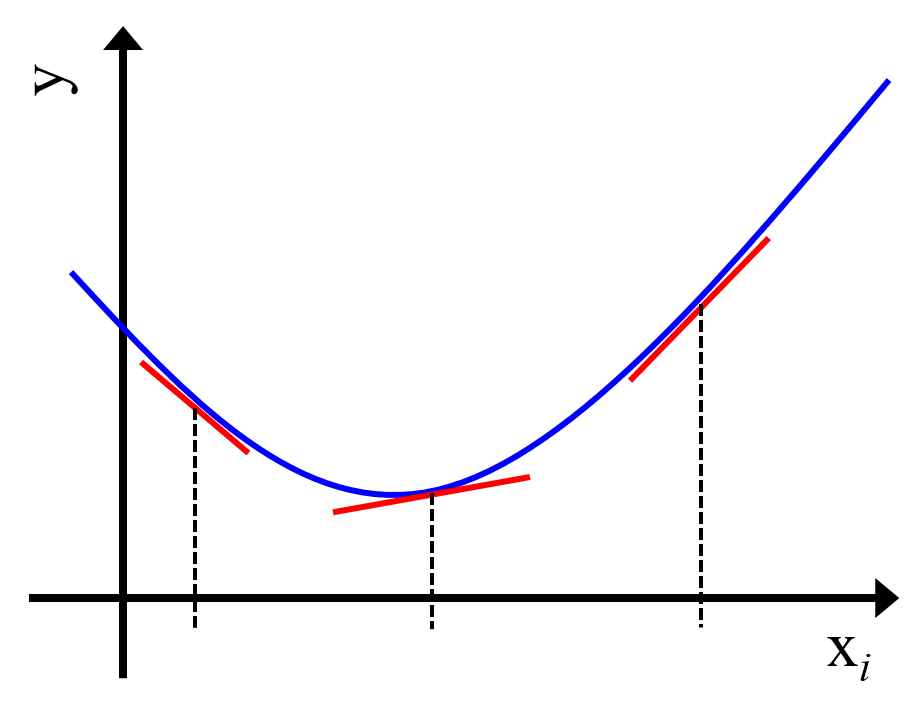
これらの指標は、いろいろな使い方ができます。しかし、非線形モデル全体の寄与ではなく、局所的な寄与を検討するとよいです。そもそもモデルが非線形なので、モデル全体で説明変数の目的変数に対する寄与が同じである必要はありません。説明変数が小さい値のときは負の寄与があり、大きい値のときには負の寄与がある、といったことも起こりうるわけです。それを (全体を平均化するなどして) 説明変数ごとに一つの寄与の値があるとするのは、意味がありません。
では指標の値を具体的にどう使うか?
指標の値により局所的にモデルを解釈するのがよいと思います。モデルの逆解析をするときに役立ちます。

たとえば、目的変数の値がより大きくなるような材料設計をしたいとき、現状で目的変数の値が最大となるサンプルの周辺で、各説明変数の指標の値を計算します。指標の値が、正もしくは負に大きい説明変数において、それと同じ方向に値を変えることで、目的変数の値を大きくできると期待できます。モデルの逆解析でも説明変数の値の設計はできますが、各説明変数の目的変数に対する局所的な寄与を検討しても、説明変数の値を設計できます。
他には、あるサンプル周辺における各説明変数の感度を見積もりたいときにも、指標の値を利用できます。たとえばモデルの逆解析で、有望そうな説明変数の値を獲得できたとします。次に知りたいのは、その値を (少し) 変化させたときに、目的変数の値はどのように変化するかです。目的変数の値があまり変化しないのでしたら問題ありませんが、大きく変化してしまうのでしたら、もう少し感度の小さい別の候補のほうがよいかもしれません。ただ、変化の方向が設計の目標と合っていたら、説明変数の値を同じ方向に動かすことで、新たな候補を探索したほうがよいかもしれません。
以上のように、非線形モデルにおける目的変数に対する説明変数の寄与を局所的に計算することで、分子設計・材料設計などの設計問題におけるモデルの逆解析に役立ちます。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


