材料設計において、材料の物性 Y と実験条件 X との間で回帰モデル Y = f(X) を構築し、そのモデルに基づいて Y が望ましい値であったり、目標の値であったり、目標の範囲に入ったりするような X の値の提案を行います。いわゆるモデルの逆解析です。


逆解析で得られた X の値で実験を行います。この実験でよい結果が得られ、例えば Y の値が目標を満たしている場合には、ゴールになりますが、そうでない場合には、その実験結果をサンプルとしてデータセットに追加して、新たに Y = f(X) を構築し、次の X の値を提案します。このモデル構築、逆解析、実験を繰り返すことで、Y の目標値となるような材料を探索します。
モデル構築、逆解析、実験を何回も繰り返して、それでも Y の目標値に達成しないと、そもそも原理的に目標を達成できない材料なのではないか、と考えるかもしれません。これ以上やっても、もう Y の値を向上できませんよ、みたいなことがデータ解析・機械学習によって分かれば嬉しいです。材料開発をストップし、次の材料の開発をはじめることができます。
しかし残念なことに、基本的にデータ解析や機械学習からは逆解析の限界はわかりません。例えば実験条件が 10 あり、それぞれの実験条件において 10 通りの設定値を振りたい場合には、すべての組み合わせは 1010 通りものとてつもなく大きな数になります。すべてを実験することはできませんし、ベイズ最適化では、

より外挿になるような次の実験条件が選択されがちですが、それでも広大な解空間をまんべんなく探索することは不可能です。次の実験条件の値が、これまでの値を超えない保証はどこにもないわけです (値を超える確率はゼロではありません)。
次の実験を行うかどうか判断するのは、人です。
では、その判断材料として、どのような情報をデータ解析・機械学習により示せるでしょうか。
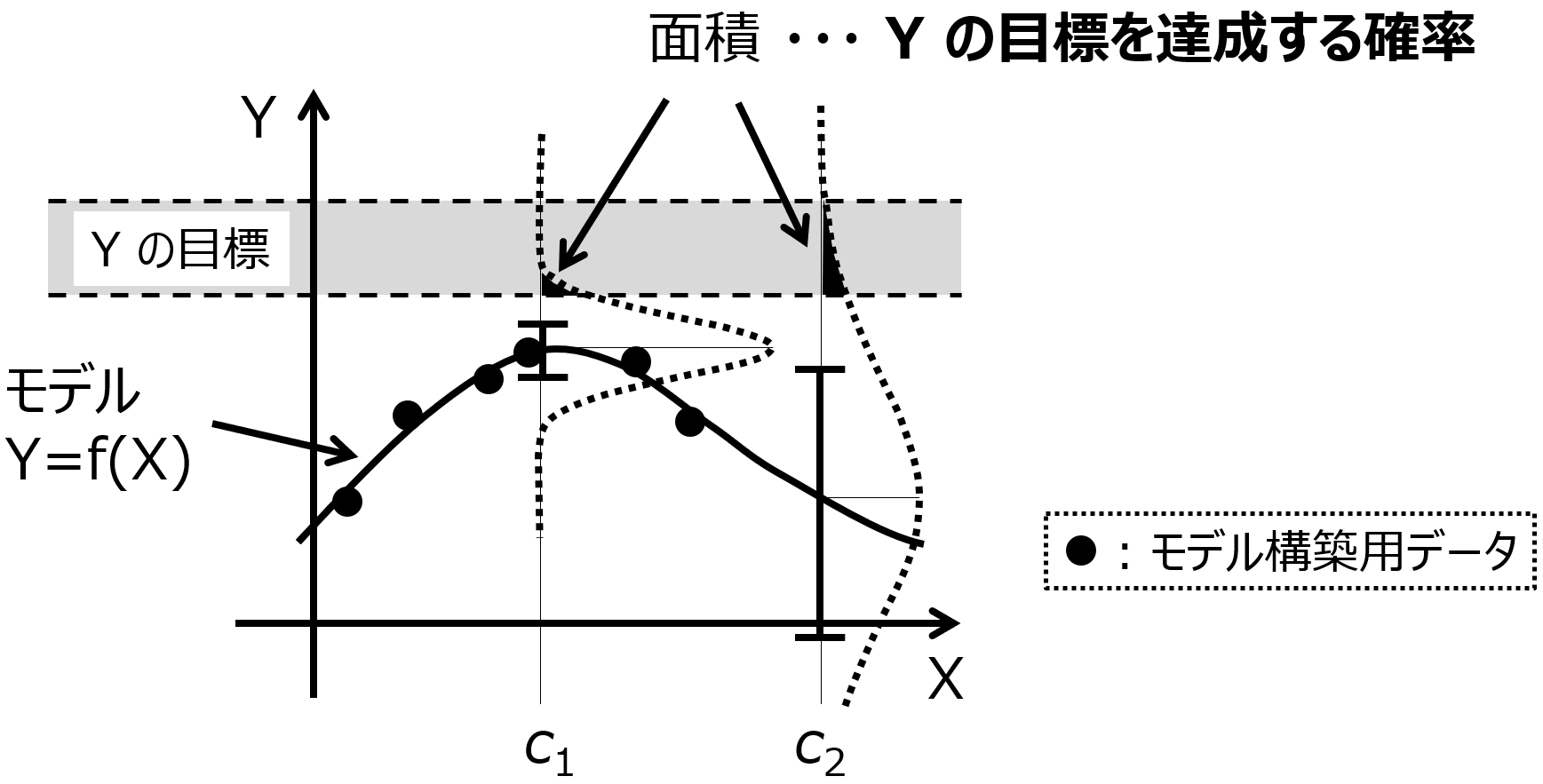
一つはモデルの適用範囲 (Applicability Domain, AD) 付きの Y の予測値です。

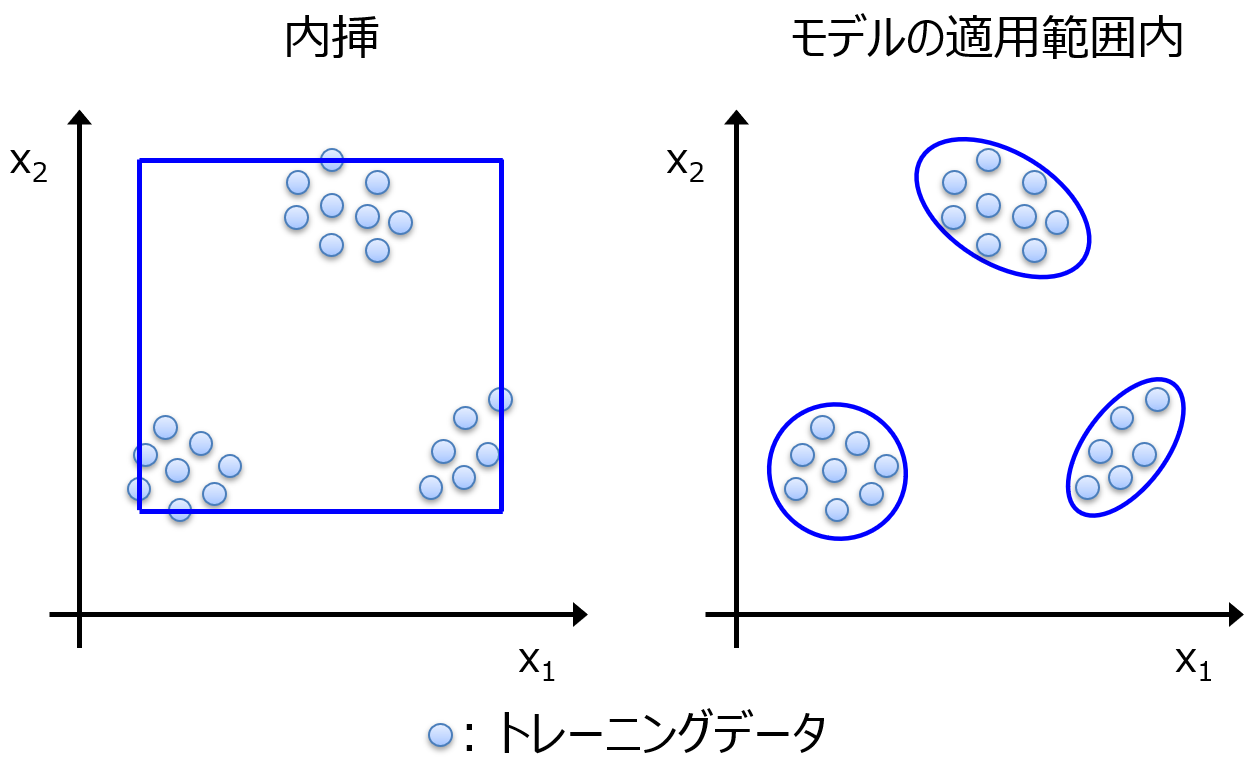
AD 内であれば、トレーニングデータにおける予測誤差と同様の誤差であると考えられますので、それを基準にして、実験後の Y の値を考え、目標を達成するかどうか、実験するかどうかを人が判断します。
また AD の情報として、アンサンブル学習における Y の予測値の分散とすることで、

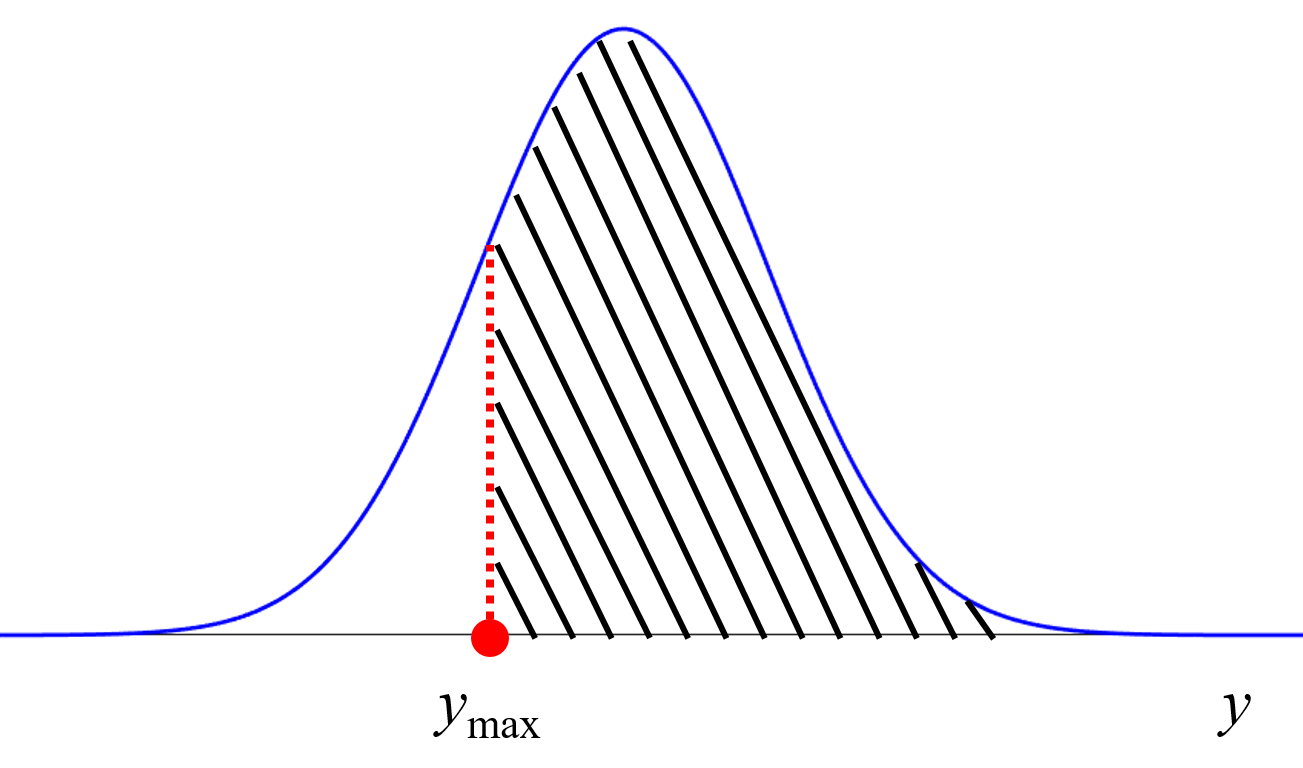
例えば予測値が正規分布に従うと仮定したとき、平均値として予測値を用いて、さらに予測値の分散を用いることで、正規分布を決められますので、例えば予測値の±2×標準偏差以内に実測値が入る確率はおよそ 95 % といったような確率で表現できます。この確率と実験にかかるコストを考え、次の実験をするかどうかを判断します。
ベイズ最適化でも確率で表現できます。Y がある目標範囲に入る確率や、ある値以上となる確率で表現することで、Y の目標を満たす確率を考えることができます。
以上のように、AD 付きの Y の予測値や Y の確率で表現することで、たとえば確率と実験するコストを考慮し、次の実験を行うか、もう実験をストップするかを考え判断することになります。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


