説明変数 x と目的変数 y の間で構築されたモデル y = f(x) を運用するとき、モデルの適用範囲 (Applicability Domain, AD) が必須になります。AD は、モデルが本来の予測性能を発揮できる x のデータ範囲です。



AD を設定する手法として、k最近傍法(k-Nearest Neighbor, k-NN) や One-Class Support Vector Machine (OCSVM) などいろいろあります。
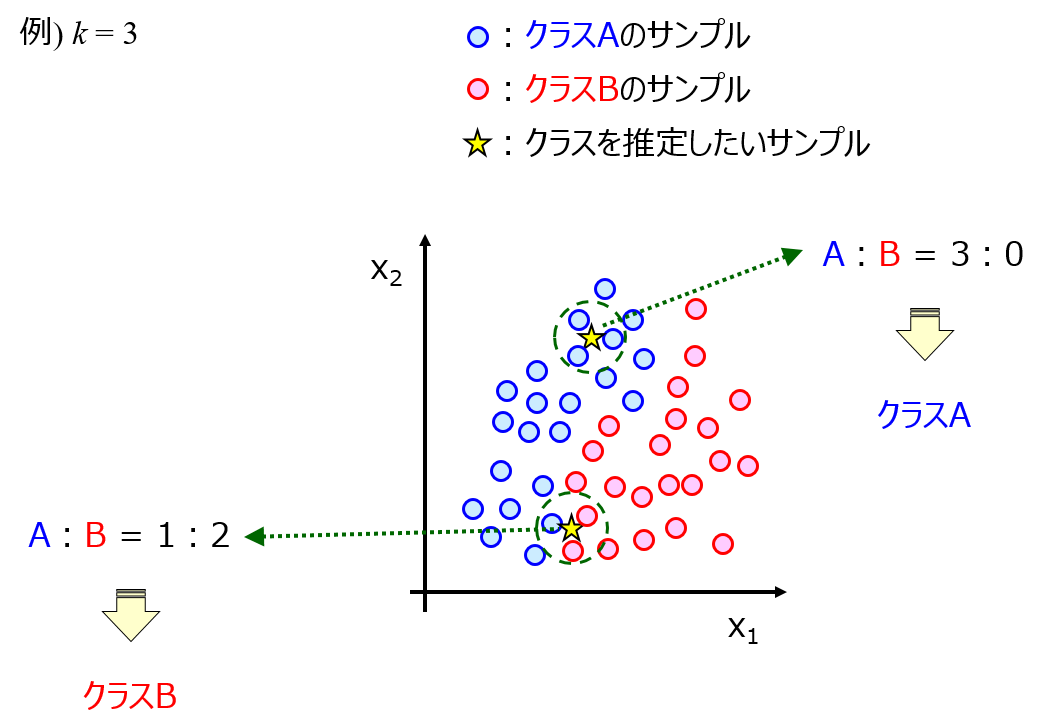
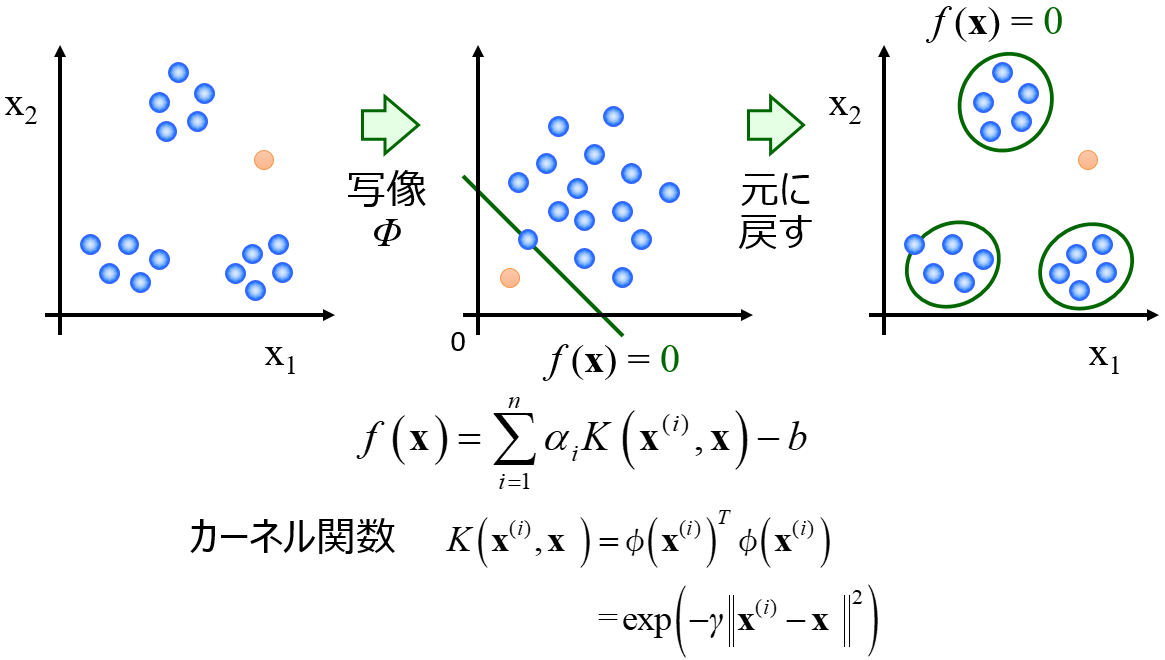
ちなみに DCEKit では k-NN、OCSVM を含む AD の計算ができます。

AD を計算するときは、AD の手法の中から一つ選んだり、その手法におけるハイパーパラメータを選んだりする必要があります。ただ AD は基本的に教師なし学習であるため、回帰分析やクラス分類といった教師あり学習のようにテストデータの予測性能やクロスバリデーションの推定性能に基づいて手法やハイパーパラメータを決める、といったことができません。
では、どのように AD の手法やハイパーパラメータを決めればよいでしょうか。まず、簡単なやり方としては、深く考えずに k-NN で k = 10 とするのでよいと思います。経験的には、これで大きな問題はありません。もちろん、OCSVM によりスパースなモデルを構築でき、次元の呪いの影響を受けにくいとされています。ただ、例えば OCSVM でガウシアンカーネルを使ったときには、パイパーパラメータが二つあり、それらの設定が難しいです。そのため、簡便に使用でき、k として妥当な値もある k-NN が妥当な選択肢といえます。
次に、より詳細に検討する方法です。回帰分析における予測誤差も用いて、Area Under Coverage and RMSE curve (AUCR) を指標にして決めます。まず、ここでいう予測誤差は、テストデータのサンプルの場合はそのまま y の誤差で OK ですが、トレーニングデータのサンプルの場合はダブルクロスバリデーションをしたときの y の誤差がよいです。

次に AUCR の計算方法についてです。まず、AD の指標を計算し、サンプルを AD の内側順に、例えば k-NN でいえば平均距離が小さい順に、サンプルを並び替えます。そして、最も小さい 30 サンプルで RMSE を計算し、次に小さい 1 サンプルを追加して 31 サンプルで RMSE を計算し、また小さい 1 サンプルを追加して 32 サンプルで RMSE を計算し、、、といったことを、すべてのサンプルで RMSE を計算するまで繰り返します。これにより、RMSE を計算したサンプルの割合と、RMSE の関係が得られます。横軸をサンプルの割合、縦軸を RMSE としたときの曲線の、下側の面積が AUCR です。
AUCR が小さいということは、AD の小さい順に y の予測誤差の小さいサンプルを整理できたということになり、AD として妥当といえます。そのため、手法を変えたり、手法におけるハイパーパラメータを変えたりして、それぞれ AUCR を計算し、AUCR が最小となる手法とハイパーパラメータの組み合わせを選ぶのがよいと思います。
なお参考情報ですが、こちらの論文では、AUCR に基づいて新たな指標を開発し、予測誤差の指標としています。

以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


