データセットを用いて、目的変数 y と説明変数 x の間で回帰モデルやクラス分類モデルを構築した後に、モデルを適切に運用するため、モデルの適用範囲 (Applicability Domain, AD) を設定します。



AD を設定する方法はいろいろあります。x の範囲に基づく方法や、データセットの x の中心からの距離に基づく方法や、x のデータ密度によって設定する方法や、アンサンブル学習によって決める方法などです。x の範囲や中心からの距離に基づく方法の問題を解決したのがデータ密度に基づく方法であるため、基本的にデータ密度やアンサンブル学習によって AD を決めることが多いと思います。
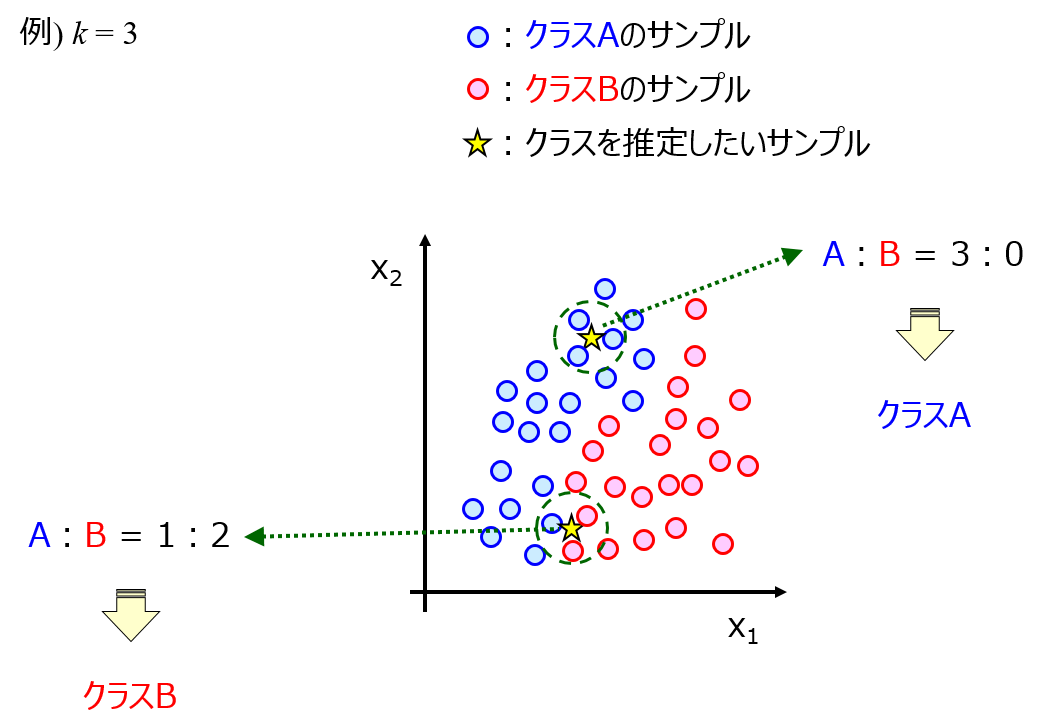
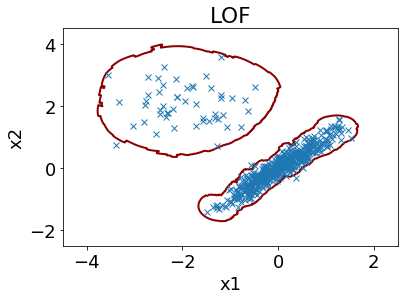
ただ、データ密度に基づく手法にも、k 近傍法や local outlier factor や One-Class Support Vector Machine (OCSVM) など、いろいろな手法があります。
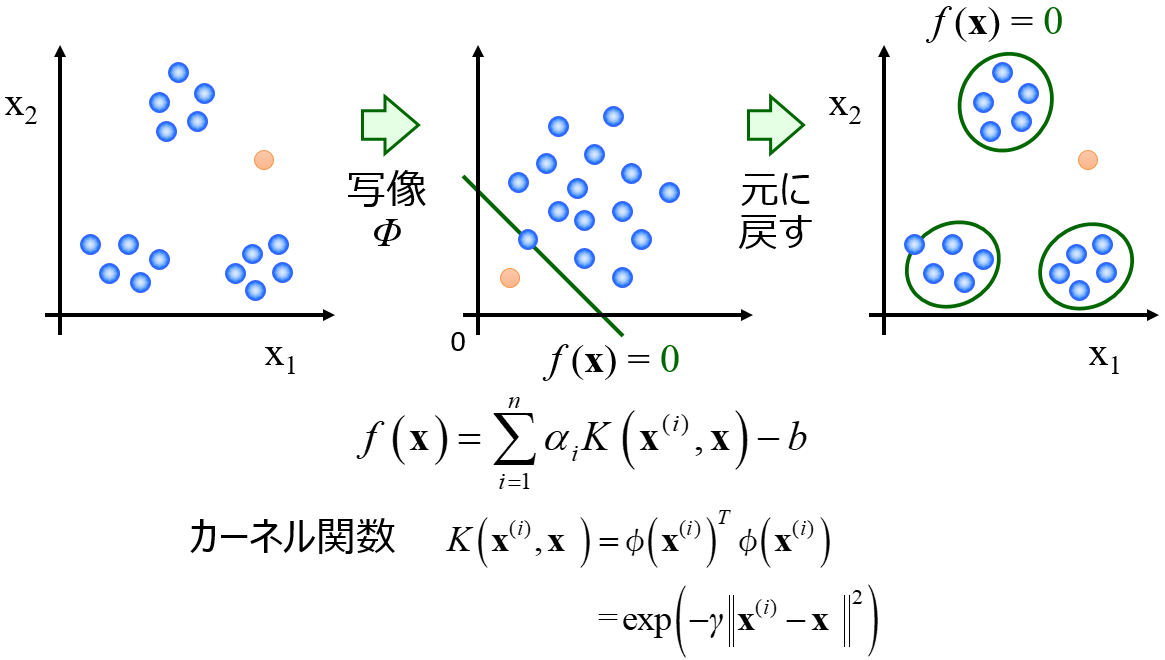
広義ではガウス過程回帰 (Gaussian Process Regression, GPR) もこの一つです。

アンサンブル学習においても、サブモデルをどの手法で構築するかによって、いろいろなパターンがあります。データ密度やアンサンブル学習に基づく AD の検討の仕方について確認します。
基本的にデータ密度に基づく手法では AD の指標として、トレーニングデータとの近さ (もしくは遠さ) に関する指標が得られる一方で、アンサンブル学習においては y の予測値の標準偏差という予測値を検討する際に使いやすい指標が得られます。y の予測誤差が正規分布に従うと仮定できれば、予測値±標準偏差以内に 68 %、予測値±2×標準偏差以内に 95 %、予測値±3×標準偏差以内に 99.7 % の確率で実測値が得られると期待できます。
データ密度に基づく指標でも y の予測値の標準偏差を求めたい場合は、データ密度の指標から y の予測値の標準偏差に変換する必要があります。例えば GPR では、サンプルあいだのデータの近さからワインの標準偏差に変換するようなやり方をしています。
AD を検討するもう一つの観点として、サンプルごとの予測誤差のばらつきを AD の指標で表現できているか、があげられます。例えばテストデータにおける y 予測結果や、ダブルクロスバリデーションを行ったときの y の予測結果を用いて、y の実測値と間の誤差を、AD の指標で評価できているか確認する必要があります。横軸を AD の指標、縦軸を予測誤差としたときに、AD の指標の値が小さいとき、もしくは値が大きいときに予測誤差は小さく、AD の指標の値が大きくなるほど、もしくは値が小さくなるほど予測誤差のばらつきが大きくなることを確認する必要があります。さらに、定量的にはこちらで説明したような方法で、いろいろな AD の手法やその中のパラメータを検討し、それぞれ適切なものを選択するとよいと思います。

以上のような AD の検討をしながら AD を設定し、評価や設計にモデルを使用するとよいと思います。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


