分子設計・材料設計・プロセス設計・プロセス管理において、分子記述子・合成条件・製造条件・評価条件・プロセス条件・プロセス変数などの特徴量 x と材料の物性・活性・特性や製品品質などの目的変数 y との間で、データセットを用いて数理モデル y = f(x) を構築し、構築されたモデルを用いて x の値から y の値を予測したり、y が目標値となるような x の値を設計したりします。
最も単純な数理モデル構築手法の一つとして、最小二乗法による線形重回帰分析があります。
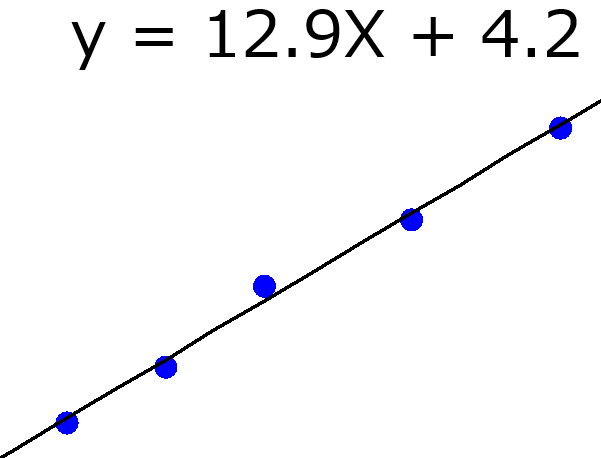
上の資料にあるように、x のトレーニングデータを X、y のトレーニングデータを y とすると、回帰係数 b は以下のように与えられます。
b = (XTX)-1XTy
予測したいサンプルの x を xnew として、予測された y の値を ypred とすると、以下のように表されます。
ypred = xnewb
この式は、上の回帰係数の式から、以下のように変形できます。
ypred = xnew(XTX)-1XTy
この式における xnew(XTX)-1XT を h とおくと、
ypred = hy
(h = xnew(XTX)-1XT)
となります。この式は、y の予測値は h と y の内積、すなわちトレーニングデータの y (y = [y1, y2, …, yn]、n はトレーニングデータのサンプル数) の値それぞれに h = [h1, h2, …, hn] の重みをつけて足し合わせたもの
ypred = h1y1 + h2y2 + … + hnyn
といえます。h1, h2, …, hn は y1, y2, …, yn の ypred に対する影響力と考えられます。h のことを leverage と呼びます。
予測したいサンプルの x がトレーニングデータの x に近いときは、重み h が極端な値とならず、どのサンプルの y の値も安定して y の予測値に影響しており、安定して y の値を予測できます。一方で、予測したいサンプルの x がトレーニングデータの x から遠いときは、重み h が異常に極端な値となり、y の予測値が不安定になってしまいます。このように、最小二乗法による線形重回帰分析におけるモデルの適用範囲 (Applicability Domain, AD) としても機能します。

なお、サポートベクター回帰 (Support Vector Regression, SVR) でも、トレーニングデータにおける y の重み付き和が予測値となります。

SVR においてどんなカーネル関数を用いても、トレーニングデータにおける y の重み付き和になるのは代わりません。非線形のカーネル関数では、重み h が線形ではなく非線形で計算されることになります。SVR では重み h の中で、サンプルによっては値が厳密に 0 になることがあり、そのような意味でスパースなモデルといえます。

SVR では、予測したいサンプルの x がトレーニングデータの x から遠くなればなるほど、重みが 0 に近づき、ついには定数項になります。
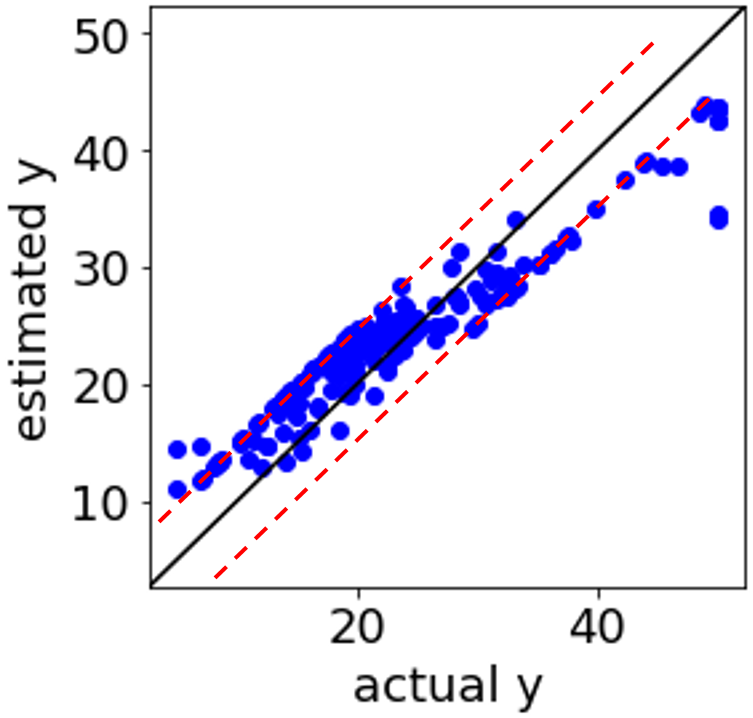
このような意味で SVR の AD としても機能しているといえます。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。


