ガウス過程による回帰をうまく使って、実験計画法における新しい実験候補を探索したり、回帰モデルやクラス分類モデルのハイパーパラメータ (学習では求まらないため事前に決めるべきパラメータ) を決定する方法が、ベイズ最適化 (Bayesian Optimization, BO) です。ガウス過程による回帰についてはこちら、実験計画法についてはこちらをご覧ください。今回はベイズ最適化について、pdfとパワーポイントの資料を作成しました。pdfもスライドも自由にご利用ください。
pdfファイルはこちらから、パワーポイント(pptx)ファイルはこちらからダウンロードできます。
興味のある方はぜひ参考にしていただき、どこかで使いたい方は遠慮なくご利用ください。
さらに、ベイズ最適化を実行するプログラムを作成しましたので公開します。ベイズ最適化のデモや、適応的実験計画法のデモも一緒です。Python や MATLAB のコードはこちらの Github にあります。
GitHub - hkaneko1985/design_of_experiments
Contribute to hkaneko1985/design_of_experiments development by creating an account on GitHub.
github.com
[New] こちらの DCEKit でもベイズ最適化をご利用いただけます。
DCEKit (Data Chemical Engineering toolKit) を PyPI にリリース！
これまで化学データ・化学工学データのデータ解析に役立つツールや金子研で開発された手法に関する Python コードを Github にて公開してきました。このたびは、これらのツール・手法 (の一部) に加えて、新たな機能を追加して、DCEK...
datachemeng.com
2019.08.18
ベイズ最適化の概要
- ガウス過程による回帰により説明変数と目的変数との間で回帰モデルを構築する
- 推定値とその分散を利用して、目的変数の値がより大きくなる(小さくなる)可能性の高いサンプル候補を見つける
- 実験計画法やハイパーパラメータの最適化に活用できる
スライドのタイトル
- ベイズ最適化 (BO) とは？
- ベイズ最適化のための準備
- ベイズ最適化をするときの前提
- ガウス過程による回帰
- 回帰モデルを用いた探索
- 獲得関数
- Probability of Improvement (PI)
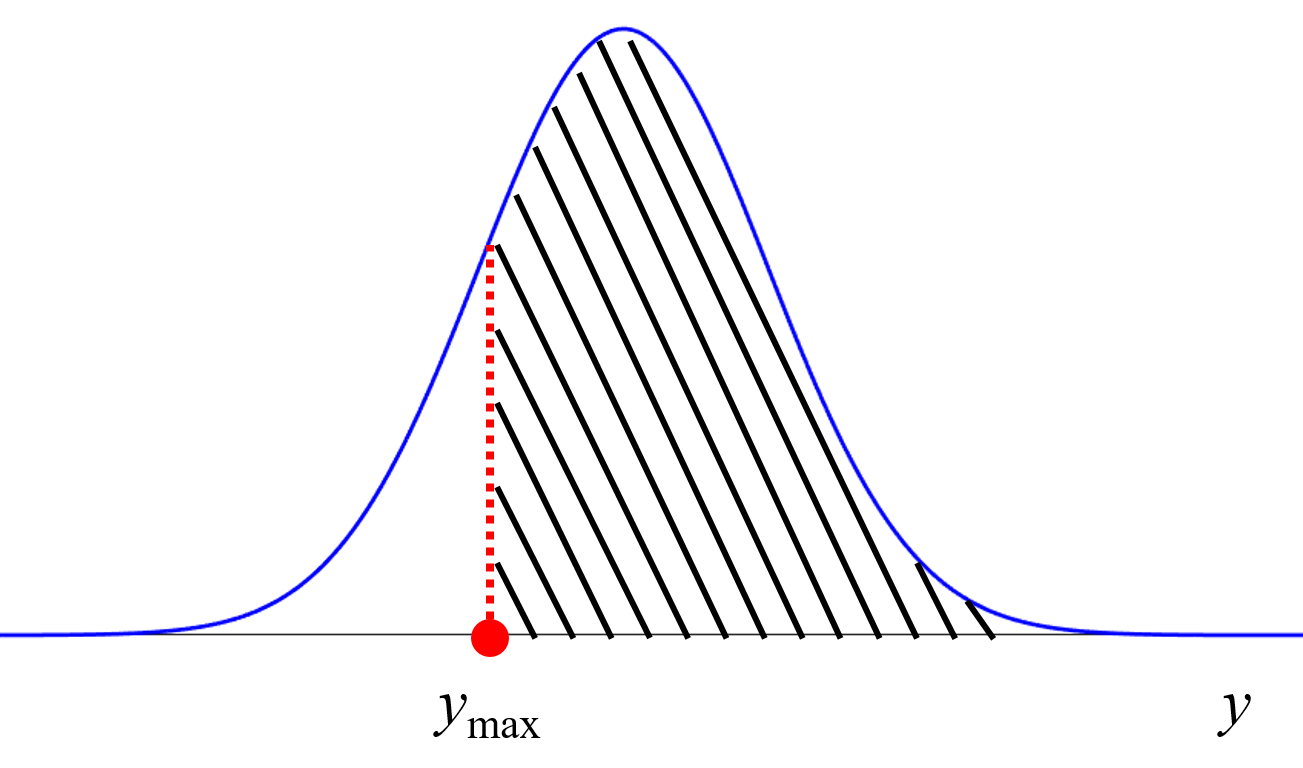
- PIの図解
- PIの式
- Expected Improvement (EI)
- Mutual Information (MI)
- 適応的な実験計画法
- サンプルの候補が多いときは？
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。
