以下の記事で紹介させていただいた、バッチプロセスの終点予測とバッチプロファイルの設計について、ここ一週間で多くの反響をいただきましたので、補足しながら丁寧に説明したいと思います。

まず今回のバッチプロセスで前提としているのは、バッチプロセスにおいて色々な材料・製品が作られるときに、バッチ時間の異なるデータが得られている状況です。バッチデータを集めたあとのデータセットとしては、以下の図のようなデータセットを想定しています。
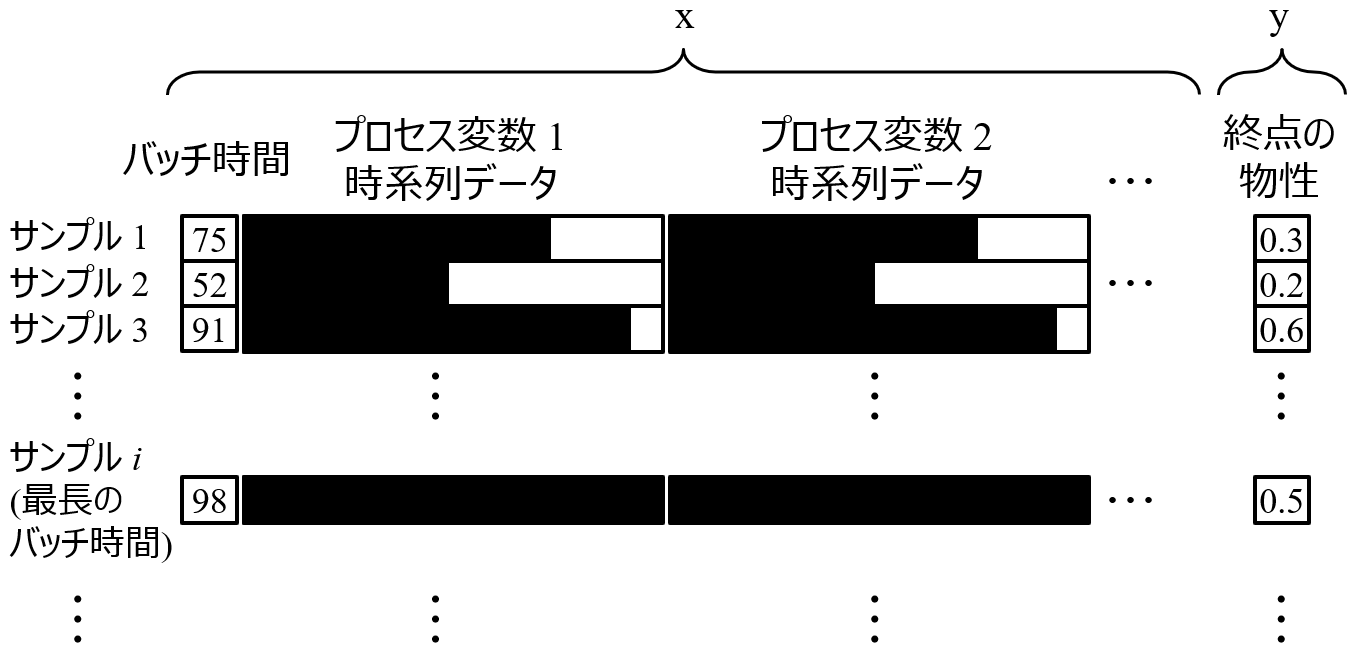
エクセルのシートのような感じで、縦に各バッチのデータ (サンプル) が並んでおり、横にバッチ時間や、プロセス変数ごとの時系列データや、終点の物性が並んでいます。時系列データの部分は、横に時刻ごとの測定値が入っており、値が入っているところが黒色になっています。白色のところは何も入っていません。バッチ時間が短いバッチは、黒色が短く、バッチ時間が長いバッチは、黒色が長いことがわかります。バッチ時間とプロセス変数ごとの時系列データをあわせて x とします。また、バッチごとに一番右に予測したいパッチの終点 y が並んでいます。
上の図では、バッチごとに一つのサンプルというような記載になっていますが、もちろんバッチの運転中に何回かサンプリングしながら物性 y を測定することもありますので、その場合はサンプリングするごとに、サンプリングまでの時間を「バッチ時間」とみなして、縦にサンプルを並べることになります。連続プロセスでも、例えば銘柄切り替え (トランジション) それぞれを「バッチ」と見立てて、上図のようにデータセットを準備することで(バッチ時間がトランジション時間になります)、トランジションの設計ができるようになります。
y を予測したりプロセス変数ごとの時系列データを設計したりする、基本的な戦術としては、直接的逆解析が可能な Gaussian Mixture Regression (GMR) で、バッチ時間・プロセス変数ごとの時系列データ・y との間で数理モデルを構築することになります。しかし、上図の白色のような値が存在していないデータセットでは、モデル構築ができません。
そこで、2通りの方法で GMR でモデル構築できるデータセットに変換します。一つは、白色の部分を補完する方法です。これは、パッチごとのプロセス変数の平均値で補完したり、バッチごとのプロセス変数の最終値で補完したり、0で保管したりしました。この中で最も良好な結果になったのは、0 で補完する場合でした。白色の部分に 0 を入力することで、x と y の間で GMR モデルを構築できます。
もう一つの方法は、フーリエ変換によって時系列データを周波数領域に変換する方法です。周波数領域で変数を揃え (ここは、ひと工夫必要です)、バッチ時間と合わせて x とすることで、x と y の間で GMR モデルを構築できます。
構築された GMR モデルに y の目標値を入力することで、バッチ時間をはじめとする x の値が直接予測できます。フーリエ変換していた場合は、逆フーリエ変換することで時系列データに戻せます。
このようにして、バッチ時間が異なる様々なデータが存在する中で GMR モデルを構築して、バッチの終点を予測したり、y が目標値となるようなバッチ時間および各プロセス変数の時系列データ、すなわちバッチプロファイルを設計したりできます。
興味ありましたらよろしくお願いいたします。
以上です。
質問やコメントなどありましたら、twitter, facebook, メールなどでご連絡いただけるとうれしいです。

