データ化学工学研究室(金子研)では、大学・企業・研究所を問わず、共同研究もさせていただきながら前に進んでいます。学生も多く在籍しており、共同研究のような広がりのある研究や他機関連携に興味のある人もおりまして、引き続き共同研究先を模索しております。
共同研究であることから我々 金子研だけでなく、共同研究先にもメリットがないといけません。
そこで、金子研との共同研究によってどんなメリットがあるのか整理いたします。
[TOC]
モデルの予測精度の向上
金子研では機械学習・インフォマティクス・データサイエンスに軸足をおいて、日々研究しています。また、分子・材料・プロセスや実際の装置・プラントといった、様々な対象のデータを用いて解析しています。データ解析や機械学習において、もちろん数理モデルの構築の仕方も重要ですが、x の検討をしたりモデルの形式を対象に合わせたりといった、分子・材料・プロセス・装置・プラントならではの解析方法も重要です。ぜひ、ご自身の実験系・製造系・シミュレーション系において、ご一緒に検討できるかと思います。
特徴量エンジニアリング
上でも述べたように、化学や工学における様々なデータを用いて日々研究をしています。データセットにおける特徴量の種類としても、分子記述子・実験条件・製造条件・合成条件・評価条件・プロセス条件・プロセス変数をはじめとして、スペクトルデータ・画像データ・時系列データ・文字データといった様々な形式のデータを扱い、解析しています。もちろん、分子・材料・プロセス・装置・プラントの対象も重要ですが、データの種類に応じて、対象にそった x を開発することも重要です。ドメイン知識と組み合わせて、一緒に特徴量エンジニアリングをすることで、モデルの予測精度や解釈性の向上ができます。
モデルの直接的逆解析
y の値から x の値を直接予測するモデルの直接的逆解析は、金子研独自の方法論・技術であり、日々研究しております。

直接的逆解析の対象も、材料の実験条件・合成条件・評価条件・プロセス条件といった、そのまま数値で表現できるデータだけでなく、分子生成と組み合わせた直接的逆解析やバッチプロセスのプロセス変数のプロファイルを予測する直接的逆解析など対象範囲を広げています。
さらに、直接的逆解析で扱うモデルの予測性能も日々向上させております。
モデルの逆解析や分子・材料・プロセスの設計にお悩みのときは、モデルの直接的逆解析を検討してみてはいかがでしょうか。
x の重要度や傾き、シミュレーション等によるモデルの解釈
モデルの構築やその逆解析だけでなく、構築したモデルの解釈も、大きな研究テーマの一つです。実際、 これまで線形モデルの解釈、大域的な非線形モデルの解釈、局所的な非線形モデルの解釈それぞれの技術を開発してきました。

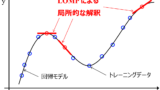
上の特徴量エンジニアリングと合わせて、新たなデータセットにおいてモデルの解釈を実施できればと考えています。
以上になります。上記の内容にご興味がありましたら、ご連絡のほどお待ち申し上げます。
質問やコメントなどありましたら、X, facebook, メールなどでご連絡いただけるとうれしいです。


